Inscription / Connexion Nouveau Sujet
produit scalaire
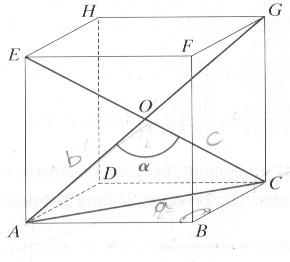
ABCDEFGH est un cube de centre O et d'arête a. L'angle AOC = α
Exprimer les longueur AC, AO et Oc en fonction de a. Montrer que l'angle α est indépendant de a
Bonjour cecilia13,
Pour le calcul de AC :
On se place dans le carré ABCD, un petit coup de Pythagore dans le triangle ABC
et on trouve
Pour le calcul de A0 :
Propriété à utiliser : O est le milieu des diagonales du cube donc
Un petit coup de Pythagore dans le triangle ACG pour calculer AG et on en déduit AO.
et on trouve
Pour le calcul de A0 :
Utilisation du caractère isométrique de la symétrie par rapport au plan contenant H, B, F et D.
Par cette symétrie OA est transformé en OC donc OC=OA
donc
pour l'indépendance de l'angle par rapport à a :
On vient de montrer que le triangle OAC est isocèle en 0
et donc comme la somme des angles dans un triangle vaut on a donc :
(*)
Mais dans le triangle ACG on a
donc la tangente de l'angle ne dépend pas de a donc l'angle
non plus et en utilisant (*) on en déduit que
est indépendant de a.
Salut 


