Inscription / Connexion Nouveau Sujet
Produit scalaire
Bonjour a tous!
MAB est un triangle et I est le milieu du segment [AB]
1.Démontrer que MA.MB (vecteurs) = MI²-1/4AB²
2. appliquer cette formule lorsque le triangle MAB est rectangle en M. Quelle propriété retrouve t-on?
3.Avec cette formule, Calculer la longueur de la médiane[MI] pour un triangle MAB tel que MA=3, MB=5 et AB=7
Ce que j'ai fait:
1.Démontrer que MA.MB (vecteurs) = MI²-1/4AB²
MA.MB=(MI+IA).(MI+IB) (relation de chasles)
=MI²+IA.MI+MI.IB+IA.IB
=MI²+MI.(IA+IB)+IA.IB
Or IA=-1/2*AB et IB=1/2*AB
Alors on a:
MI²+MI.(0)-1/2AB*1/2AB
=MI²-1/4AB²
2.dans le cas d'un triangle rectangle en M, le produit scalaire MA.MB =0
donc
MI²-1/4AB² = MA.MB
MI²-1/4AB² = 0
(Mais je vois pas comment poursuivre)
Bonjour,
2)MI²-1/4AB² = 0
donc MI²=(1/4)AB² et MI = AB/2
propriété de la médiane d'un triangle rectangle....
MI²-1/4AB²=0
MI²-1/4AB²=0
MI-1/2AB=0
MI=1/2AB
c'est inexact..... car
il faut d'abord écrire
MI² = (1/4)AB²
puis
(MI² )= [(1/4)AB²]
et
MI = AB/2
C'est le théorème suivant :
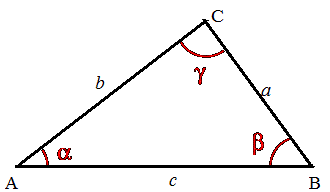
Soit un triangle ABC, dans lequel on utilise les notations usuelles exposées sur la figure :
d'une part α, β et γ pour les angles et, d'autre part, a, b et c pour les longueurs des côtés respectivement opposés à ces angles.
alors
c² = a² + b² - 2abCos
Annuler
connectez vous