Inscription / Connexion Nouveau Sujet
Produit scalaire
Bonjour j ai une activité à faire en maths ; mais je ne comprend rien ! En effet c'est pour découvrir le cours ....
Si vous pouviez m'aider !
L'énoncé est le suivant :
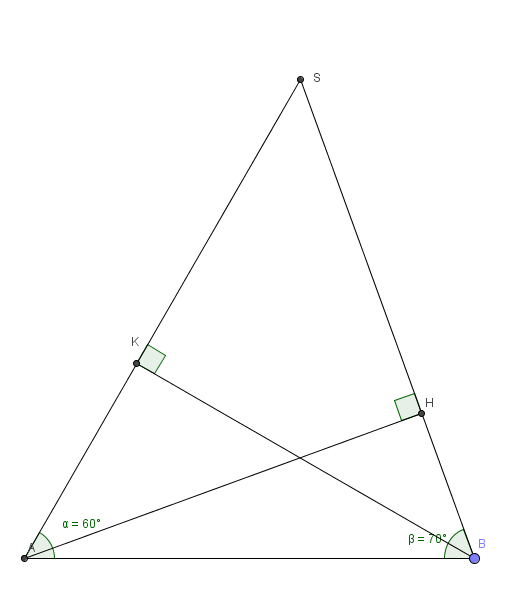
Une antenne relais pour les téléphones portables dont la portée est de 30 km doit être placée sur le sommet S d'une montagne. Dans la vallée au pied de cette montagne se trouve 2 villes À et B distantes en ligne droite de 27 km . On souhaite savoir si l'on pourra capter le signal de l'antenne dans chacune des deux villes.
Il est impossible de mesurer les distances SA et SB par contre on a pu mesurer les anges ABS et BAS on a obtenu ABS = 70 degres et BAS = 60 degres .
1) précises la mesure de l'angle ASB
2) à) dans le triangle ABs on note h le pied de la hauteur issue de À montrer que AH=AB sin 70 degres =AS sin 50 degres
B) en déduire une valeur approchée de AS
3 ) à) on note k le pied de la hauteur issue de B montrer que BK = BA si I 60 degres =BS SIN 50 degres
B) en déduire une valeur approche de BS
4) préciser pour chacune des deux villes si l'on pourra ou non capter le signal de l antenne relais
5) à l aide des résultats dès questions précédents comparer les rapports (AB/ sin 50) ,(AS/ sin 70 ), et ( BS/ sin 60 )
Bonsoir
qu'avez-vous trouvé ?
cela ne fait appel qu'à la définition du sinus dans un triangle rectangle
question 1
que vaut la somme des angles d'un triangle ?
question 2
Quelle est la nature du triangle AHB ?
d'accord pour 2 c'est le texte il n'y a rien à montrer
dans le triangle ABS on note H le pied de la hauteur issue de A
D'accord mais pour trouver AS ? Je dois calculer le produit scalaire mais comment m'y prendre?
Pour la 3 je procède pareille ?
non il n'y a pas de produit scalaire ici
utilisez la définition du sinus dans un triangle rectangle
comme je vous l'avais déjà écrit
En effet; je me suis trompée dans mes calculs ... Merci !
Donc pour la 4) on ne capte que dans la ville B
Pour la 5) les rapports tourne tous autour de35 !