Bonjour,
la seule chose que tu peux affirmer avec ces égalités de vecteurs
est : c'est un parallélogramme

et d'ailleurs si alors (Chasles) obligatoirement

pour en dire plus il faut d'autres conditions que des égalités de vecteurs :
produits scalaires nuls ou pas pour les angles éventuellement droits.

D'accord

AB . AC = 2,7 * 6,7 - 7,2 à ( -5,7) = 59,13 0

Il n'y a pas d'angle droit en A donc ce n'est ni un carré et rectangle

Si ABCD est un parallélogramme, alors on peut dire que c'est également un quadrilatère.
La proposition C et F

Bonsoir,

comme te l'a écrit mathafou, tu as regardé des égalités de vecteurs et non de longueurs.
Donc ABCD est un parallélogramme

par ailleurs , tu écris

il faut faire attention à l'ordre des sommets
ABCD, c'est en "tournant autour" dans cet ordre là

implique ABCD parallélogramme dont les côtés sont AB, BC, CD et AD
si on avait eu
ce serait un quadrilatère croisé (et ABDC serait un parallélogramme, pas ABCD)

les diagonales sont AC et BD
calculer c'est chercher l'angle entre un coté et une diagonale
ça ne sert pas à grand chose ce produit scalaire là ...
ce qui se "voit" sur une figure comme préconisé par co11

D'accord
Il n'y a pas d'angle droit dans un parallélogramme ( quadrilatère )

il faut comprendre la "hiérarchie" des quadrilatères :
un carré est une sorte de rectangle qui est une sorte de parallélogramme qui est une sorte de quadrilatère.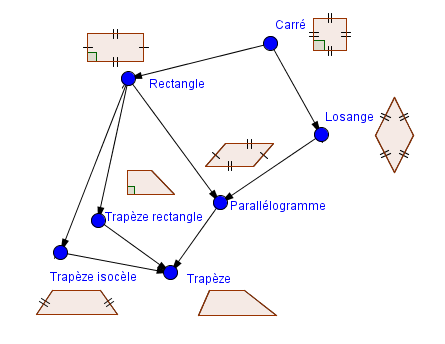


les flèches indiquent ceux qui sont "une sorte de" ce qui est en dessous

quand on a trouvé que c'est "un parallélogramme"
il faut chercher s'il n'y a pas plus précis
est ce un rectangle ou pas ?
puis si c'est un rectangle, est ce un carré ou pas

(et puis si ce parallélogramme n'est pas un rectangle, peut être est ce un losange ou pas, qui est aussi "une sorte de parallélogramme")

D'accord
Donc ce parallélogramme est une sorte de rectangle car AB = DC et AD = BC

Si un quadrilatère a les quatre côtés de la même longueur alors c'est un losange et si les diagonales d'un quadrilatère se coupent en leur milieu et sont perpendiculaires alors c'est un losange

Ici ce n'est pas la cas car les 4 côtés ne sont pas égaux.

Donc ABCD est un quadrilatère, rectangle et parallélogramme ?

il faut arrêter obligatoirement d'écrire de la même façon les vecteurs et les mesures de longueur.
au pire si tu ne sais pas mettre des flèches tu écris vAB pour parler du vecteur et AB pour parler de la mesure de longueur.


cela veut dire AB = CD (longueur ) et parallèles et de même sens

ça suffit à dire : ABCD est un parallélogramme. (sans préciser de quelle sorte)
cours de collège : un quadrilatère( convexe) qui a DEUX côtés parallèles et égaux est un parallélogramme.
ici le "convexe" est à cause de "de même sens"

et par conséquent ses deux autres cotés BC et AD sont aussi parallèles et égaux (en longueur)
totalement inutile de comparer et
c'est une conséquence de ce qu'on sait déja et ça n'apporte absolument rien de plus.

pour savoir si c'est un rectangle ou pas il faut faire un test supplémentaire qui correspond à une propriété de collège (traduite en vecteurs / coordonnées) qui distingue les parallélogrammes non rectangles de ceux qui le sont.
revoir le cours de collège au besoin.
et ce n'est certainement pas "les deux autres cotés sont aussi parallèles et égaux" vu que c'est vrai quel que soit le parallélogramme, qu'il soit rectangle ou pas !

donc tu n'as toujours pas prouvé que c'est un rectangle ou pas

J'ai dit que ABCD est un parallélogramme car vAB =v DC et vBC = vAD

Un quadrilatère qui  a 2 côtés parallèles et égaux est un parallélogramme ( BC = AD )

Si un quadrilatère a des diagonales de même longueur et qui se coupent en leur milieu / si un parallélogramme a un angle droit / si un parallélogramme a des diagonales de même longueur . Alors c'est un rectangle
J'ai calculé AC = 8,79 et BD = 8,10, c'est donc différent

On peut dire que le parallélogramme n'est pas rectangle, sauf erreur

ABCD est un parallélogramme car vAB =v DC et ça suffit
et vBC = vAD inutile

J'ai calculé AC = 8,79 et BD = 8,10
tu n'en avais rien dit et donc tu faisais des affirmations sans preuve
"sauf erreur"
oui, il y a erreur.

et de toute façon ce n'est pas sur des valeurs approchées décimales qu'il faut faire un tel test, c'est sur les valeurs exactes (racines carrées écrites )
(et vu que par le passé tu as parfaitement montré que la précision des calculs et toi ça fait deux)
ou comparer les carrés des longueurs.

oui désolée j'ai calculé des longueurs

Jusqu'ici j'ai trouvé que c'est un quadrilatère et parallélogramme.
Je suppose qu'il en manque :
je n'ai pas réussi à démontrer que c'est un rectangle ou non malgré les calculs des diagonales AC et BD

que ABCD soit un quadrilatère n'est pas un scoop !
OK pour parallélogramme

ensuite
ton calcul de diagonales est faux (des erreurs de calcul)
montre en détail comment tu le fais...

D'accord

AC ( 11,5 - 4,8 ; 10,7 - 16,4 )
AC ( 6,7 ; - 5,7 )
AC = 6,7² + (-5,7)² = 8,79

BD ( 7,5 - 8,8 ; 9,2 - 17,2 )
BD ( - 1,3 ; - 8 )
BD = (-1,3)² + (-8)² = 8,10

énoncé :
B (7,5 ; 9,2)
D (8,8 ; 17,9)
vecteur BD (xD - xB; yD - yB) toi tu calcules DB (xB - xD; yB - yD)
ce n'est pas grave car la norme sera la même.
mais tant qu'à faire autant écrire correctement

DB (7,5 - 8,8; 9,2 - 17,9)
cette erreur de recopie d'une valeur de l'énoncé dans ton calcul ne pardonne pas ...

Désolée c'est une erreur d'inattention

DB (7,5 - 8,8; 9,2 - 17,9)
DB ( - 1,3 ; - 8,7 )

DB AC
Peut-on dire que ce parallélogramme n'est pas rectangle ?

Rectification :

Les normes de DB = AC
                                8,79 = 8,79

Peut-on dire que ce parallélogramme est rectangle ?

Au total, je recense :

ABCD : quadrilatère, rectangle, parallélogramme

Je comprends bien, mais ma calculatrice affiche directement la valeur approchée sans passer par l'intermédiaire des valeurs exactes ()

tu n'as pas compris du tout ce que j'ai dit
il ne faut PAS extraire la racine carrée à la calculette du tout

pour comparer DB et AC
on écrit
ça reste écrit comme ça et c'est une valeur exacte
même 8.7965902484996992157131052885331... ne serait pas une valeur exacte

de la même façon que n'a jamais été égal à 1.4142135623730950488016887242097
et encore moins à 1.41
est et rien d'autre.


idem, ça reste écrit comme ça
et là sur ces valeurs exactes on a bien
vu que exactement 77.38 = 77.38

c'est à dire que on ne compare pas AC et BD mais AC² = BD² = 77.38 (exactes)

par ailleurs je tiens à signaler que il y a plusieurs façons de résoudre cet exo
parce qu'il y a plusieurs critères différents permettant de savoir si c'est un parallélogramme, un rectangle etc

avec le thème "produit scalaire", "les diagonales sont égales " et "les cotés adjacents sont inégaux" n'est pas un critère judicieux en phase avec le thème de l'exo

"un parallélogramme dont deux côtés adjacents sont perpendiculaires est un rectangle" est bien plus "en thème"
et ça se fait avec le produit scalaire
(et l'avantage : il n'y a pas de racines carrés dans un tel calcul...

idem : "un rectangle dont les diagonales sont perpendiculaires est un carré" donc là aussi un produit scalaire

en résumé :

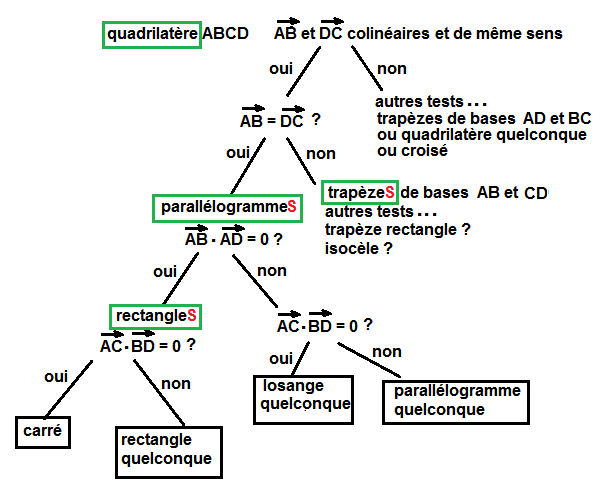
D'accord
AB peut être égal à DC ou non.
Si oui, dans ce cas c'est un parallélogramme. Donc ce n'est pas un trapèze. Dans votre résumé, vous aviez encadré le trapèze en vert

la procédure est générale
les encadrés (vert ou pas) ne sont pas les solutions de CET exo, mais les diverses conclusions que l'on peut apporter en général

D'accord,
Donc dans cet exercice, il y a 3 solutions : quadrilatère, parallélogramme et rectangle.

il y a trois cases à cocher et une seule solution
c'est un rectangle un point c'est tout

ce qui en fait ipso facto un parallélogramme et bien entendu un quadrilatère (!!)

D'accord,
Merci beaucoup de m'avoir aidé.