Inscription / Connexion Nouveau Sujet
Produit scalaire
 Tulipe18
Tulipe18Bonjour,
Voici l'exercice:
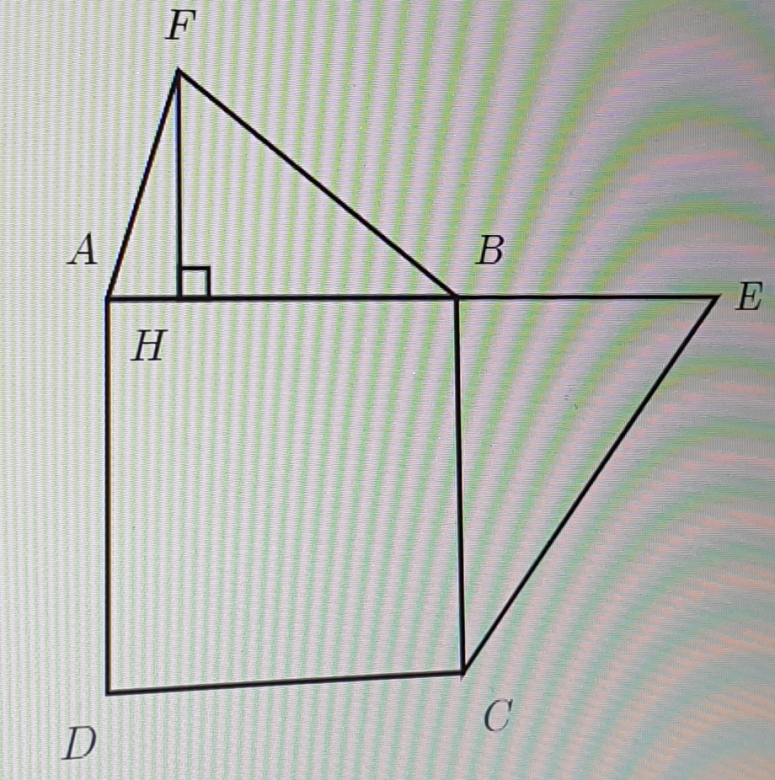
On considère la figure ci-dessous, où :
ABCD est un carré
FH = 3
AB = 5
BE = 4
AH = 1
BCE est rectangle en B
Calculer le produit scalaire
→ →
CF ⋅ AF
J'ai fait plusieurs méthodes et à chaque fois je trouve -4. Or, cet exercice est un QCM. Les réponses proposées sont:
20; -25; 18; 42
Pouvez-vous m'aider ?
Merci par avance
1ère méthode :
CF . AF = CF . AH (car H est le projeté de F sur (AB))
CF . AH = (CB + BF) . AH = (CB + BH) . AH = (CE + EB + BH) . AH = (BE + EB + BH).AH ( car B est le projeté de C sur (BE))
= BH . AH = - ||BH|| × ||AH|| = -4 × 1 = -4
(car BH et AH sont colinéaires de sens opposés)
(Tout est en vecteur)
2ème méthode:
CF . AF = (CA+AF).AF = (CA+AH).AH = (CD+AH).AH = CD.AH+||AH||^2 = BA.AH+||AH||^2 = 1/2 (||BA+AH||^2-||BA||^2-||AH||^2)+||AH||^2 = 1/2(||BH||^2-||BA||^2-||AH||^2)+||AH||^2 = 1/2(4^2 - 5^2 -1^2)+1^2 = -4
Bonjour,
erreur fondamentale
CF . AF = CF . AH (car H est le projeté de F sur (AB))
complètement faux de chez faux
la méthode avec les projetés orthogonaux concerne la projection d'un des vecteurs sur le support de l'autre
exclusivement
pas sur une droite quelconque n'importe laquelle !!
on aurait par exemple
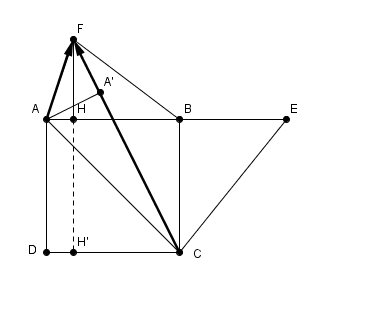
avec A' la projection de A sur (FC)
CF.AF = CF.A'F
ce qui n'apporte pas grand chose ...
2ème méthode:
CF . AF = (CA+AF).AF OK Chasles
= (CA+AH).AH AH n'est pas AF, ni la projection sur va savoir quoi ... (même erreur)
bonnes méthodes :
formule avec les longueurs : calculer (Pythagore) ||AF||, ||CF|| et ||AC||
et appliquer la bonne formule
ou bien par décomposition (selon les directions du carré car cela conduira à des simplifications)
CF.AF = (CB+BF)(AH+HF) par Chasles
= CB.AH + CB.HF + BF.AH + BF.HF développement
CB.AH = 0
CB.HF = ||CB||*||HF|| car colinéaires de même sens
BF.AH , là oui on peut projeter l'un sur le support de l'autre
BF.HF, et là aussi
ou bien calcul via des coordonnées et un repère
etc etc
Bonjour,
J'ai repris mon exercice avec les 3 méthodes que tu me donnes. Avec un repère, je trouve bien 20. Avec les autres méthodes, je bloque toujours.
Méthode du repère:
(D,i,j) le repère: D l'origine et i, j les vecteurs unitaires
D(0,0) ; C(5;0); B(5;5) ; A(0;5); H(1;5); F(1;8); E(9;5)
Puis j'ai calculé les coordonnées des vecteurs CF(-4;8) et AF(1;3)
Donc CF.AF = -4*1+8*3 = 20
Méthode de décomposition et projeté orthogonal:
CF.AF = (CB+BF).(AH+HF) (Relation de Chasles)
= CB.AH+CB.HF+BF.AH+BF.HF (Développement)
= 0 + IICBII*IIHFII+BH.AH+BH.HF
(Car: CB et AH sont perpendiculaires; CB et HF sont colinéaires de même sens; BH et AH sont colinéaires de sens contraires; H est le projeté de F sur (AB))
CF.AF = IICBII*IIHFII-IIBHII*IIAHII + 0
(Car: BH et AH sont colinéaires de sens contraire et BH et HF sont perpendiculaires)
CF.AF= 5*3-4*1 = 15-4 = 11
Où est mon erreur? C'est toujours les projections ???
Méthode des longueurs et Pythagore:
Je n'arrive pas à calculer IICFII puisque le triangle CBF est isocèle en B mais rectangle donc on ne peut pas utiliser Pythagore ?
• coordonnées OK
• BF.HF ≠ BH.HF
tu projettes BF sur le support de HF ???? certainement pas ! toi tu le projettes sur (AB) donc c'est faux
la méthode avec les projetés orthogonaux concerne la projection d'un des vecteurs sur le support de l'autre
exclusivement
pas sur une droite quelconque n'importe laquelle !!
• Par Pythagore : je t'ai tracé un point H' c'était pour l'utiliser !!
Bonjour ;
Une autre façon de faire :
***message modéré***heureusement que tu sais le faire ! ***merci de laisser faire les élèves !!**
ça revient exactement au même
au lieu de projeter un vecteur on le remplace par Chasles avec le point de projection orthogonale
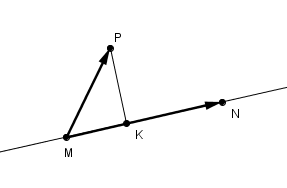
MN.MP = MN(MK+KP) = MN.MK + MNKP = MNMK + 0 = MN.MK
on démontre ainsi la propriété énoncée par projection d'un vecteur sur le support de l'autre.
il me semble même que vu que Tulipe18 n'arrête pas de se tromper quasiment à chaque fois dans ses projections, il vaudrait mieux pour lui ne jamais utiliser nulle part cette propriété directement, et les remplacer systématiquement par cette décomposition supplémentaire

 )
)
