Inscription / Connexion Nouveau Sujet
Produit scalaire
Bonjour
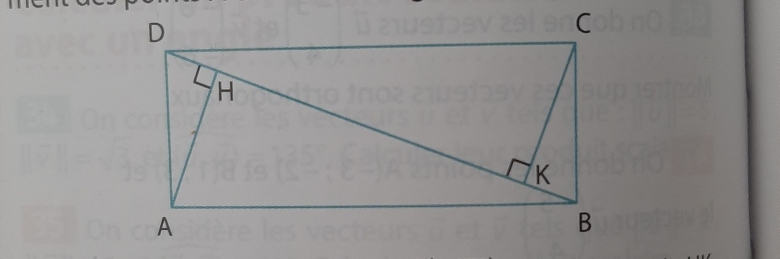
on considere un rectangle ABCD tel que AB=7 et AD=3 les points H et K sont les projetes orthogonaux respectivement des points A et C sur la diagonale BD
1)Exprimer le produit scalire AC.DB en fonction de HK en utilisant la projection j'ai trouvé AC.DB=HK.DB
=HK*DB
2) en utilisant DB=DC+CB calculer autrement ce meme produit scalaire j'ai trouvé 40
3) en deduire la valeur excacte de la longueur HK
j'ai fait
AC.DB=HK*DB=40
HK*10=40
HK=4
mais je ne suis pas sur
Merci
oui je me suis dis pareil j'ai fait
Ac=AB+BC
DB=DC+CB
donc AC.DB=(AB+BC).(DC+CB)
=(AB.DC)+(AB.CB)+(BC.DC)+(BC.CB)
=AB*DC-BC*CB
car AB.CB ET BC.DC sont nul car orthogonaux
=7*7-3*3
=40
Tu n'as pas l'impression que si tu voulais aller du point D au point B, ce serait faire un détour que passer par le point C ?
Autrement dit, la ligne droite est le plus court chemin d'un point à un autre.
Dit plus mathématiquement, la longueur du côté d'un triangle est inférieure à la somme des longueurs des deux autres côtés.
Ici, dans le triangle BDC, on a BD < DC+CB.
Bon, maintenant, pour calculer la longueur BD :
Quelle est la nature du triangle BDC ?
Annuler
connectez vous