Inscription / Connexion Nouveau Sujet
Produit scalaire
Bonjour, je suis bloqué à un exercice, j'aimerais avoir votre aide. C'est sur le produit scalaire :
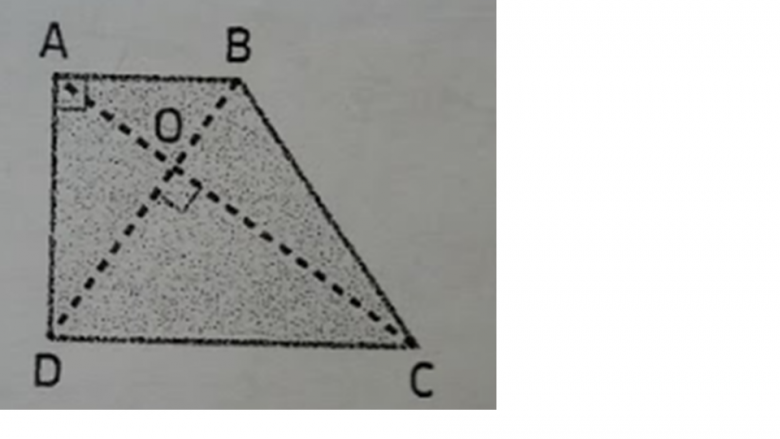
ABCD est un trapèze de bases [AB] et [DC], qui est rectangle en A et dont les diagonales [AC] et [BD] sont perpendiculaires et se coupent en O.
On a AB = 3 et AD = 4
1) En calculant de deux façons différentes, en déduire que OB =
Je l'ai fait de 2 façons différents et pour j'ai trouvé 9
Mais je n'arrives pas à déterminer OB...
La longueur [BD] = 5
2) Déterminer OD
3) Calculer CD, puis AC
4) Déterminer les produits scalaires suivants :
Voici l'image :
Merci de votre aide
Bonjour,
Tu as trouvé (grâce au projeté orthogonal de D sur [AB] je suppose) que
Maintenant, peut-être utiliser la formule pour déterminer le cos puis un petit coup de trigo de 3e dans AOB devrait permettre de trouver BO assez facilement...
Je l'ai fait de 2 façons différents et pour
Par contre, je serais curieux de connaître tes deux façons... (projeté orthogonal et ?)
Bonjour,
Je l'ai fait de 2 façons différentes
montre les détails de tes calculs
car c'est dans ces détails que l'on va trouver OB
si tu ne le vois ps, c'est que tu n'as pas choisi les bonnes "deux façons différentes"
l'une doit faire intervenir OB (et être incapable de donner une valeur numérique du produit scalaire)
l'autre doit donner la valeur numérique
en comparant les deux, on obtient OB (directement, sans trigo d'ailleurs, fausse piste la trigo et le cosinus)
c'est le principe général de toutes ces "en calculant de deux façons différentes" partout et toujours, dans cet exo comme ailleurs.
manu_du_40 mathafou
Pour la première "technique" j'ai d'abord calculer [DB] avec Pythagore ( j'ai trouvé 5) puis j'ai fais :
Pour la deuxième technique j'ai utiliser le projeté orthogonal...
D'accord.
Pourquoi pas. Ta première "technique" est correcte mais en pratique, on ne l'utilise pas très souvent au lycée.
Comme suggéré par mathafou, tu peux reprendre ma formule de14:36 et même te passer du calcul explicite de en remplaçant directement
ce qui permet de trouver BO directement.
Par contre, la trigo de 3e me semble indispensable dans tous les cas pour utiliser la définition que je viens de donner.
le projeté orthogonal... lequel ? de D sur (AB) ? détails ?
aucune de ces méthodes n'utilise OB
donc il faut une troisième méthode au lieu de l'une inutile de ces deux là
indice :
les deux méthodes attendues utilisent toutes deux des projetés orthogonaux...
donc les deux méthodes attendues sont
un projeté orthogonal
et un autre projeté orthogonal !
ceci dit je laisse manu_du_40 poursuivre.
(sans cosinus du tout, très inutilement compliqué et en dehors de "l'esprit" de cet exo)
ceci dit je laisse manu_du_40 poursuivre.
(sans cosinus du tout, très inutilement compliqué et en dehors de "l'esprit" de cet exo)
Pas de souci mathafou, tu peux intervenir autant que tu veux, je ne suis pas du genre à me formaliser du fait que je sois le premier. De plus, nos deux façons de voir les choses sont complémentaires je trouve.
Le très inutilement compliqué me semble quand même exagéré...
Pour l'esprit de l'exo, je ne sais pas...
manu_du_40 mathafou
J'ai bien compris le fait de passer par la trigo de manu_du_40 mais je ne vois pas le projeté orthogonal... Vous me conseiller de passer par la trigo ou le projeté orthogonal ( que j'ai pas encore trouvé) ? Au vu de l'exercice je devrais passer par le projeté...
D'accord.
Pourquoi pas. Ta première "technique" est correcte mais en pratique, on ne l'utilise pas très souvent au lycée.
Comme suggéré par mathafou, tu peux reprendre ma formule de14:36 et même te passer du calcul explicite de
Par contre, la trigo de 3e me semble indispensable dans tous les cas pour utiliser la définition que je viens de donner.
D'accord.
Pourquoi pas. Ta première "technique" est correcte mais en pratique, on ne l'utilise pas très souvent au lycée.
Comme suggéré par mathafou, tu peux reprendre ma formule de14:36 et même te passer du calcul explicite de
Par contre, la trigo de 3e me semble indispensable dans tous les cas pour utiliser la définition que je viens de donner.
On a :
Ce n'est pas égal à 9/2...
J'ai du faire une erreur ?
Les deux méthodes sont correctes. A mon avis, tu peux choisir celle que tu veux.
En fait, ce que t'explique mathafou, c'est que tu peux calculer BA.BD de deux façons en utilisant deux projetés orthogonaux différents.
D'après ton post de 15:19, tu en as trouvé un (lequel ?)
Si tu ne vois pas l'autre, utilises la formule avec le cos. C'est tout aussi efficace.
l'angle n'est pas de 45°
(inutilement compliqué disais-je)
pour moi l'ensemble de tous les produits scalaires de tout l'exo se font de façon homogène par cette même technique des projections orthogonales
c'est de ça que je parle à propos de "l'esprit de l'exo" 
pour cette question de calculer OB en utilisant le produit scalaire BA.BD :
1ère expression de ce produit scalaire :
une ligne, par projection de D sur (AB), donne = AB² = 9
2ème expression du même produit scalaire :
une ligne et une seule, par projection aussi (mais de quoi ? )
(faisant intervenir OB explicitement)
3ème ligne : l'égalité des deux expressions donne directement OB , terminé
(on connait BD = 5, Pythagore, une ligne déja faite)
je sors pour éviter des cacophonies,
je ne reviendrais éventuellement que quand ce sera calculé correctement.
par une méthode ou l'autre.
manu_du_40
comment voulez-vous résoudre ceci alors qu'on a seulement la longueur BA ?
D'où sors tu que
Je pensais que l'angle était coupé en 2 donc la moitié de 90°. En revanche je ne vois pas le projeté de mathafou j'ai trouvé
Pas besoin de connaître la valeur de
Il te suffit d'écrire
Pour la méthode de mathafou.
Penses que
mathafou manu_du_40
Complètement faux. Cela ne marche que si ton triangle est rectangle ET isocèle
manu_du_40
D'accord je ne savais pas pour le triangle rectangle.
On a :
9 = 3 5
5
BO =
2) On sait que [BD] = 5 et [BO] = donc [OD] = [BD] - [BO]
= 5-() = 3.2
[OD] = 3.2
3) Calculer CD, puis AC
Là je ne vois pas trop...
Qu. 1 : OK même si la simplification (par BA) aurait pu être faire dès le début. Cela aurait évité des calculs inutiles
Qu.2 : Attention de rester rigoureux dans les notations.
Pas de crochets lorsqu'on parle de longueurs.
Qu. 3 : Pour CD, Thalès peut-être ?
manu_du_40
D'accord pas de soucis 
Pour Thalès
on peut remplacer par les données :
j'utilise le produit en croix :
(3.2 3)/1.8 =
3)/1.8 =
DC =
Ensuite pour calculer AC je peux appliquer le théorème de Pythagore dans le triangle ADC rectangle en D ? On connait AD = 4 et DC =
C'est correct ? Donc :
Dans le triangle ADC rectangle en D on a :
AC ²= DC²+ DA²
AC² = ()² + 4² =
AC =
4) Je peux commencer les produits scalaires ?
C'est correct mais avant de commencer la question 4, il faut d'abord simplifier cette racine dans la longueur AC
manu_du_40
Oui elle est égale à
Je suis entrain de me poser une question. Pour appliquer le théorème de Pythagore dans ADC, il faut un triangle rectangle, mais rien me dit qu'ADC est rectangle en D. Il y a pas des propriétés particulières qui dise ceci dans un trapèze ?
Il y a pas des propriétés particulières qui dise ceci dans un trapèze ?
C'est quoi la définition du trapèze ?
Et celle du trapèze rectangle ?
manu_du_40
Je ne connais pas la définition, mais je sais que AB est parallèles à CD.
DA est perpendiculaire a AB
Il y a une propriété qui dit que quand 2 droites sont parallèle et que une droite est perpendiculaire à l'une alors elle est perpendiculaire à l'autre,
donc j'ai la réponse à ma question?
Tu as en effet la réponse à ta question.
Sinon, la définition d'un trapèze :
c'est un quadrilatère qui a deux côtés parallèles. Ces côtés sont appelés bases du trapèze.
manu_du_40
Ok.
Pour les produits scalaires, on a :
AB = 3 ; AD = 4 ; AC = { DC =
BD = 5 ; OD = 1.8; OD =3.2
car ce sont 2 vecteurs orthogonaux.
=
= 4² = 16
= ?
=
= 4² = 16
=
= 5² = 25
Est-ce correct ? Je n'ai pas trouvé pour
J'ai fais que du projeté orthogonal.
Merci de votre aide
Le dernier est faux
le projeté orthogonal de sur (BD) n'est pas
: où y a-t-il un angle droit qui permettrait de projeter l'un des deux vecteurs sur la droite support de l'autre ?
les deux calculs sont liés, é, é,
tous les deux sont faux car tu ne vois toujours pas la projection de quoi que ce soit sur la droite (BD).
que ce soit maintenant, ni jadis dans la question 1
est même "visiblement faux" car cela voudrait dire que
et
sont orthogonaux,
donc que (BC) serait parallèle à ... (AC) !! (deux perpendiculaires à une même droite ...)
mathafou
Bonjour,
pour =
Pour , je suis passer par la formule avec 3 points.
J'explique :
=
(BD²+BC²-DC²)
On a BD = 5 et DC =
Il nous manque BC, on va pouvoir le trouver grâce a Pythagore dans le triangle BOC rectangle en O.
D'abord il nous faut OC,
OC = AC - AO
On va chercher AO
Dans le triangle AOB rectangle en O on a :
AO = =
( je le rappel, AB = 3 et OB = 1.8)
AO =
AC - AO = -
=
Donc OC est
On peut appliquer Pythagore dans le triangle BOC rectangle en O afin de trouver BC :
(BC est l'hypoténuse)
BO²+OC² = BC²
1.8²+² = BC²
= BC² donc
=
On a maintenant tous ce qu'il nous faut :
On a BD = 5 et DC = et BC =
=
(BD²+BC²-DC²)
=
=9
Pour les 2 produits scalaires que j'ai trouvé auquel j'ai eu faux précédemment, je penses qu'ils sont correct cette fois-ci, qu'en pensez-vous ?
Je vous remercie 
que de complications inutiles !
c'est la même projection pour les deux !
se projette en
sur la droite (BD)
donc,
ou comme tu l'as fait avec les valeurs décimales puisque par chance ce sont des nombres décimaux (exacts)
et pour l'autre :
donc oui, tes résultats sont justes (je n'ai pas vérifié les calculs intermédiaires)
pour la question 1 c'était d'ailleurs encore la projection sur O qu'il était judicieux d'utiliser :
se projette en
sur (AB) donc
comme déja vu
mais ensuite se projette en
sur (BD)
donc,
donc 5*BO = 9 et BO = 9/5 immédiatement sans aucun besoin de quelque cosinus que ce soit


