Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première Produit scalaireTopics traitant de Produit scalaire [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

Produit scalaire

Posté par
Azerty43690 29-12-20 à 10:36

Bonjour,
je ne comprends pas à quoi correspond l'intervalle de k

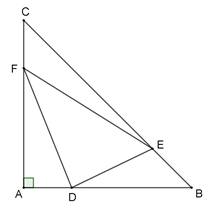
On se place dans le repère orthonormé (A ,(AB) ⃗,(AC) ⃗)

Les points D, E et F sont placés sur les segments [AB], [BC] et [CA] tels que

AD=BE=CF=k   avec  k∈[0 ;1]



1)Déterminer en fonction de k les coordonnées des points F et D

2)Montrer que les coordonnées du point E sont :

E (1-k √2/2;k √2/2)

3)Calculer le produit scalaire (DE) ⃗.(DF) ⃗ en fonction de k.

4)Existe-t-il une valeur de k telle que le triangle DEF soit rectangle en D ?

Posté par
Azerty43690re : Produit scalaire 29-12-20 à 10:40

schéma

Produit scalaire

Posté par
heklare : Produit scalaire 29-12-20 à 10:44

Bonjour

AD= k   donc \vec{AD}=k\vec{AB} si vous prenez k en dehors de cet intervalle D n'appartient plus au segment [AB]

Posté par
carpediemre : Produit scalaire 29-12-20 à 10:44

salut

tu as fait la question 2/ ... mais et la 1/

une fois les coordonnées des points connues il est aisé d'avoir les coordonnées des vecteurs DE et DF  et leur produit scalaire ...

Posté par
Azerty43690re : Produit scalaire 29-12-20 à 10:59

Oui mais comment trouver les coordonnées

Posté par
heklare : Produit scalaire 29-12-20 à 11:04

Vous avez déjà les coordonnées de D

Que vaut AF ?

Posté par
Azerty43690re : Produit scalaire 29-12-20 à 11:06

Les coordonnées de D sont AD = k AB ?

AF = k AC

Posté par
carpediemre : Produit scalaire 29-12-20 à 11:07

ça ne veut rien dire ...

on demande un couple de réels ...

Posté par
Azerty43690re : Produit scalaire 29-12-20 à 11:12

AF = CF-AF  

Posté par
carpediemre : Produit scalaire 29-12-20 à 11:14

c'est l'idée ... mais cette égalité est fausse ...

Posté par
Azerty43690re : Produit scalaire 29-12-20 à 11:17

hekla @ 29-12-2020 à 10:44

Bonjour

AD= k   donc \vec{AD}=k\vec{AB} si vous prenez k en dehors de cet intervalle D n'appartient plus au segment [AB]


D'abord je n'ai pas bien compris cela

Posté par
heklare : Produit scalaire 29-12-20 à 11:19

Dire que le point M a pour coordonnées (x~;~y) dans le repère (O ; \vec{\imath},\vec{\jmath})  c'est dire que \vec{OM}=x\vec{\imath}+y\vec{\jmath}

Posté par
heklare : Produit scalaire 29-12-20 à 11:28

  Les points A, B, D sont alignés
Si vous avez

k<0   alors D n'appartient pas au segment [AB] il est situé sur la demi-droite d'extremité A

k=0 alors D=A

0<k<1  D appartient au segment ]AB[

k=1 alors \vec{AD}=\vec{AB} et D=B

si k>1 D appartient à la demi droite [AB)  mais à l'extérieur du segment

Posté par
Azerty43690re : Produit scalaire 29-12-20 à 11:31

coordonnées:
D ( k ; 0 )
F (0 ; 1-k)

Posté par
heklare : Produit scalaire 29-12-20 à 11:43

Bien

Posté par
Azerty43690re : Produit scalaire 29-12-20 à 11:54

Par contre pour trouver x du point E il faudrait faire le projeté orthogonal de E sur la droite AB ?

Posté par
heklare : Produit scalaire 29-12-20 à 11:58

(AB)  AB \in\R

et sur (AC)

Posté par
heklare : Produit scalaire 29-12-20 à 11:59

pour (AC) c'est évidemment pour l'ordonnée

Posté par
Azerty43690re : Produit scalaire 29-12-20 à 12:01

AC = 1

Posté par
heklare : Produit scalaire 29-12-20 à 12:03

Oui

Posté par
Azerty43690re : Produit scalaire 29-12-20 à 12:05

Donc BC = 2

Posté par
heklare : Produit scalaire 29-12-20 à 12:08

Non
Revoir Pythagore

Posté par
Azerty43690re : Produit scalaire 29-12-20 à 12:08

2 plutôt

Posté par
heklare : Produit scalaire 29-12-20 à 12:09

Oui

Posté par
Azerty43690re : Produit scalaire 29-12-20 à 12:15

Mais pourquoi multiplier k par / 2

Posté par
carpediemre : Produit scalaire 29-12-20 à 12:22

on a immédiatement par la relation de Chasles : AE = AB + BE

donc les coordonnées de E sont aisées à obtenir ...

Posté par
heklare : Produit scalaire 29-12-20 à 12:23

Il faut commencer par nommer les projetés orthogonaux de E sur (AB) par exemple H et  celui de E sur (AC) par exemple L

Après deux possibilités

Soit Thalès  pour calculer EH

Soit Pythagore dans le triangle rectangle isocèle EHB

Posté par
heklare : Produit scalaire 29-12-20 à 12:24

Le problème ne donne pas le même résultat (1-k ; k)

Posté par
Azerty43690re : Produit scalaire 29-12-20 à 13:49

BE/BC = EH/CA
k/racine2 = EH/1
EH = k/racine2

CE/CB = EL/AB
(racine2-k)/racine2 = EL/1
EL =( racine2-k)/racine2

Posté par
heklare : Produit scalaire 29-12-20 à 13:54

EL=AH=\dfrac{\sqrt{2}-k}{\sqrt{2}}  oui

Posté par
heklare : Produit scalaire 29-12-20 à 13:57

EH=AL=\dfrac{k}{\sqrt{2}}  oui  à rendre rationnel le dénominateur

Posté par
Azerty43690re : Produit scalaire 29-12-20 à 14:39

c'est à dire à rendre rationnel ?

Posté par
heklare : Produit scalaire 29-12-20 à 14:47

\dfrac{a}{\sqrt{b}}=\dfrac{a\sqrt{b}}{b}

On dit que l'on a ainsi rendu rationnel le dénominateur en multipliant le numérateur et
le dénominateur par \sqrt{b} pour ne plus avoir de racine carrée au dénominateur

Posté par
carpediemre : Produit scalaire 29-12-20 à 14:53

\vec {AE} = \vec {AB} + \vec {BE} = \vec {AB} + \dfrac {BE} {BC} \vec {BC} donnait immédiatement le résultat ...

Posté par
Azerty43690re : Produit scalaire 02-01-21 à 16:03

EL=(2-racine2*k)/2

Posté par
heklare : Produit scalaire 02-01-21 à 16:26

EL est l'ordonnée de E

Posté par
Azerty43690re : Produit scalaire 02-01-21 à 18:58

l'abscisse plutôt

Posté par
heklare : Produit scalaire 02-01-21 à 19:04

Oui au temps  pour moi  l'ordonnée c'est EH

Posté par
Azerty43690re : Produit scalaire 03-01-21 à 08:23

Oui mais par contre je ne trouve pas la même chose que l'exercice

Posté par
heklare : Produit scalaire 03-01-21 à 11:11

E a pour abscisse  \dfrac{2-k\sqrt{2}}{2}=1-k\dfrac{\sqrt{2}}{2}

Pour ordonnée  k\dfrac{\sqrt{2}}{2}

C'est bien ce que donnait votre texte.

Posté par
Azerty43690re : Produit scalaire 03-01-21 à 13:50

Donc DE.DF = k2-k+1

Posté par
heklare : Produit scalaire 03-01-21 à 14:39

\vec{DE} \ \dbinom{1-k\dfrac{\sqrt{2}}{2}-k}{k\dfrac{\sqrt{2}}{2}}

\vec{DF}\ \dbinom{0-k}{1-k}


\vec{DE}\cdot \vec{DF}=\left (1-k\dfrac{\sqrt{2}}{2}-k\right)(-k)+{\left(k\dfrac{\sqrt{2}}{2}\right)(1-k)

Posté par
Azerty43690re : Produit scalaire 03-01-21 à 16:51

Donc DE.DF= k2+1/2*k*(racine2 -2)

Posté par
heklare : Produit scalaire 03-01-21 à 17:12

Oui


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1674 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !