Inscription / Connexion Nouveau Sujet
Produit scalaire
Bonsoir,
J'ai un Dm en maths et je bloque sur une question ce qui m'empêche de continuer la suite de l'exercice.
Voici mon sujet:
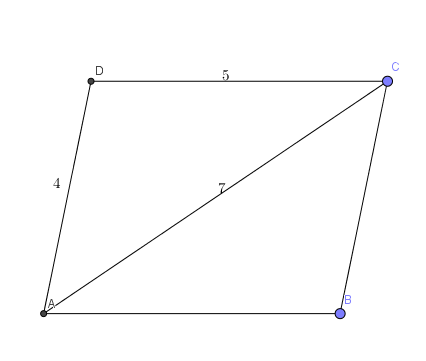
Soit ABCD un parallélogramme tel que AB=5; AD=4 et AC=7.
Nous cherchons le produit scalaire de AB x AD ( le x est normalement un point)
Merci d'avance de votre aide.
Je vois donc je dois commencer par mesurer les deux angles mais j'ai un problème c'est que je connais pas la formule pour les calculer :/
Je ne vois pas la trace d'un cosinus ; au temps pour moi il ne s'est pas affiché à cause d'une espace manquante
il faut écrire l'exposant entre les balises sup à défaut ^
bonsoir à vous deux
pour le cas où le théorème d'Al Kashi ne serait pas encore dans le cours de clarisse1,
peut-être (vect(AB)+vect(AD))² =
je repars...
Bonsoir carita
Vous pouvez rester. C'est une bonne idée simple et rapide beaucoup plus que ce que j'avais proposé
Si clarisse1 ne veut pas se lancer dans de longs calculs approximatifs
donc on efface tout et on recommence
Vous avez bien fait d'intervenir je m'étais embarqué dans de longs calculs alors que votre
proposition tient en à peine une ligne car on n'est pas obligé de recalculer un carré scalaire
Le calcul
D2=a2+c2-2xaxcxcos(ADC)
49=25+16-40xcos(ADC)
-40cos(ADC)=41-49
Cos(ADC)=5
Non?
Soit 78.5 degré
Non vous avez 49=41-40 \cos D donc
ce qui entraîne
Mais il vaut mieux abandonner ceci et utiliser ce que propose carita
Suite à ça, nous devons faire le calcul suivant:
AB . AD= ABxAD+cos(DAB)
AB . AD= 5x4+(-1/5)
AB . AD= 20-1/5
AB . AD= -4
Est-ce que c'est la bonne réponse ?
Vous avez un peu tout mélangé
Je vous ai dit d'abandonner la première méthode que je vous ai indiqué celle de carita est bien plus simple et presque sans calcul
on a donc
sachant aussi que
Oui cela m'a bien donné 1/5 avec la formule de Carita .
Mais après avoir calculer l'angle DAB. Nous devons calculer le produit scalaire de AB . AD?
C'était une erreur de passer par le calcul des angles
vous ne tenez compte que du message de 10 : 35 corrigé à 10 :36
On vous définit bien à un moment donné le produit scalaire par
par conséquent
et aussi les opérations
etc
Ce sont ces propriétés que l'on a utilisées
De rien
Pour comparer avec ce que je vous avais suggéré prochain message