Inscription / Connexion Nouveau Sujet
produit scalaire
Bonjour svp pourriez vous m'aidez:
ABCD est un rectangle tel que AB= 8 et BC=3
Les points I et J sont les milieux respectifs des segments [AB] et [BC]
1) Calculer les produits scalaires suivants:
a) CI*AD b) IJ*CD c) IB*ID d) AI*JD
2) Calculer également AB*IJ et BC*IJ
3) en déduire le produit scalaire AC* IJ
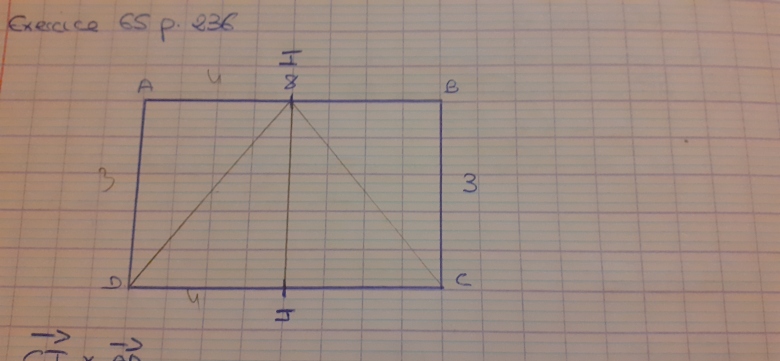
j'ai juste fais le schéma mais je ne sais pas comment procede au calcul car j'ai l'impression que mon schéma est faut (la position des lettres)
on te dit J milieu de BC ...
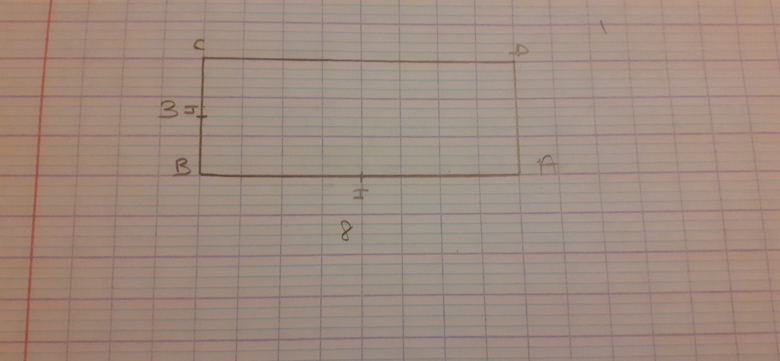
refais ton dessin (pour plus de facilité, respecte le nombre de carreaux (tu as mis 5 carreaux pour une longueur de 3),
et mets AB en bas...
le produit scalaire CI.AD s'écrit en vecteurs
quand tu décomposes avec Chasles, c'est en vecteurs
comme je te le disais plus haut : développe ! (distribue vec AD)
arrete d'écrire en majuscules, stp.
en effet
en vecteurs :
CI. AD = CB.AD + BI.AD
à présent regarde sur ton schéma : BI et AD sont perpendiculaires, que vaut BI.AD ?
et CB et AD sont // : que vaut CB.AD ??
liloudu94226,
tu n'as pas fini CI.AD !
est ce que tu lis bien mes messages ?
CI. AD = CB.AD + BI.AD
à présent regarde sur ton schéma : BI et AD sont perpendiculaires, que vaut BI.AD ?
et CB et AD sont // : que vaut CB.AD ??
donc au final CI.AD = ???
non, tu ne lis pas bien les aides !
Quand deux vecteurs sont orthogonaux, leur produit scalaire est nul.
donc
ensuite, tu passes des vecteurs aux segments sans faire attention.
Le produit scalaire concerne des vecteurs !
sont colinéaires et de sens contraire,
donc
et
il faut vraiment que tu fasses attention à ne pas confondre le produit scalaire entre vecteurs, qu'on note avec un . et un produit de longueur de segments, noté avec *
la démarche : on a décomposé un vecteur pour avoir finalement uniquement des vecteurs orthogonaux ou //
à présent
décompose le vecteur IJ en introduisant B,
développe, et regarde quels sont les vecteurs orthogonaux et les vecteurs //.
vas y !
Madame poir le vecteur 1 il faut
Calculer CI :
on a : ABC un triangle rectangle
et I milieu de AB
et d'âpres le théorème de Pythagore:
on a : CI² = CB²+BI²
CI² = 3²+4²
CI² = 9+16
CI² = 25
CI = 5
donc : CI = 5
liloudu94226,
que vient faire "calculer CI" ici ?
est ce que tu lis ce que j'écris ?
on te dit de calculer les produits scalaires :
il ne s'agit pas de CI*AD mais de
décompose le vecteur IJ en introduisant B,
développe, et regarde quels sont les vecteurs orthogonaux et les vecteurs //.
vas y !
liloudu94226,
que vient faire "calculer CI" ici ?
est ce que tu lis ce que j'écris ?
on te dit de calculer les produits scalaires :
il ne s'agit pas de CI*AD mais de
je viens de t'écrire un pavé, ou je te montre comment calculer ce produit scalaire, qui vaut -9.
lis attentivement, stp, sinon, on va avoir du mal à aller au bout...
je suis passée à la question b) qui suit la même démarche.
b)
décompose le vecteur IJ en introduisant B,
développe, et regarde quels sont les vecteurs orthogonaux et les vecteurs //.
vas y !

 :)
:)
