Inscription / Connexion Nouveau Sujet
produit scalaire
Bonsoir, est-ce possible d'avoir de l'aide pour un exercice de math sur les produits scalaires ?
ABC est un triangle. Les points M et N sont tels que : AM =3/4 AB et CN = 1/4 CA
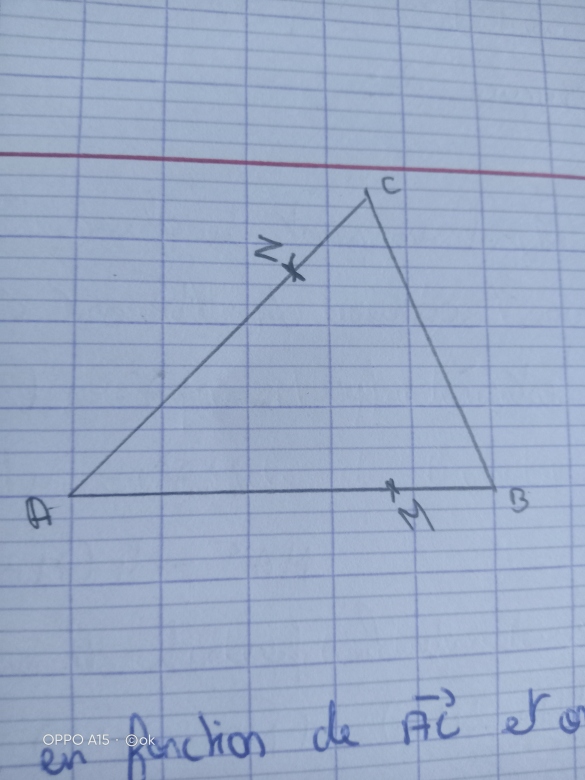
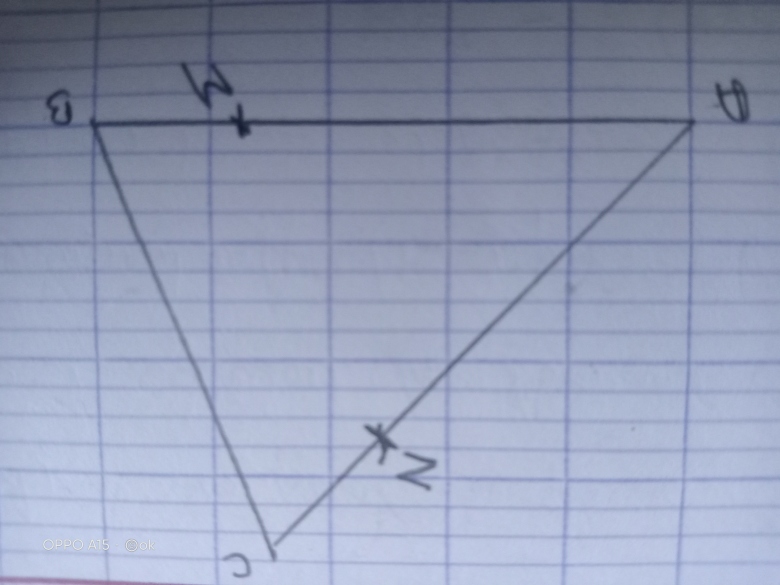
1. Réaliser une figure et placer les points M et N.
2. Exprimer AN en fonction de AC
.
3. En déduire une expression de MN en fonction de AB et AC
.
4. Justifier que les vecteurs MN et BC sont colinéaires. Que peut-on en déduire ?
Merci d'avance et précision : il s'agit de vecteur difficulté a placé les flèches des vecteurs donnés .
salut
je ne vois nulle part de produit scalaire .. et ce que tu postes est du niveau seconde !!
donc qu'as-tu fait ?
indication : relation de Chasles
carpediem
salut
je ne vois nulle part de produit scalaire .. et ce que tu postes est du niveau seconde !!
donc qu'as-tu fait ?
indication : relation de Chasles
En effet ce n'est pas du produit scalaire , erreur de ma part (mais exo inclus dans le dm )
Bonsoir
Qu'avez-vous effectué ?
Quel est le problème ?
J'ai fais les 2 premières questions et la il me reste que les 2 dernièrees
Bonjour,
juste en passant ... (je laisse hekla poursuivre)
la question 3 dit "en déduire"
c'est à dire utiliser la réponse de la question 2
quelle est ta réponse à cette question 2 ?
et puis question 1 "faire une figure" : tu peux la montrer au besoin
 extrait de
extrait de Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?
(nota : inutile de citer pour répondre)
Bonjour
Où en êtes-vous ?
On vous a fait calculer ou on vous a donné
Il serait peut-être judicieux de décomposer en passant par A.
Voici ce que j ai fais pour ma figure
Et pour la 2 : AN=AC+1/4CA
AN=AC-1/4AC
AN=3/4AC
Pouvez vous m'aider pour les deux dernières questions svp ?
bonsoir en attendant le retour de hekla à qui je rendrai la main
oui
MN=-3/4 AB + 3/4 AC OK
ne peux tu pas mettre 3/4 en facteur ?
et - AB = ??
On vous a déjà presque tout donné.
vous êtes arrivé à
je vous ai rappelé que
Quels que soient les points E et F
par conséquent
On applique la relation de Chasles et on aboutit au résultat
et pour la 4 il faut que MN et BC soit colinéaires c'est-a dire que MN+BC = 0 ?
Voici ce que j'ai fais :
MN-3/4= BC
3/ 4BC - 3/4 =BC
BC=BC ? j'ai l'impression que c'est faux pouvez vous me montrez svp
Deux vecteurs et
sont colinéaires si et seulement si, il existe un réel
tel que
ou
vous venez de montrer que donc les vecteurs sont
Que peut-on déduire de cette colinéarité ?
Je ne sais pas , donc la MN=3/4 BC et donc ils sont colinéaires ? on peut en déduire qu'ils sont parallèles ? est ce sa ? si non de m'expliquer svp , pouvez vous ainsi me montrer les étapes qui justifie que MN et BC colinéaires svp je n'arrive pas a aboutir
Oui, les vecteurs sont colinéaires. C'est une définition de la colinéarité, celle que je vous ai écrite dans le message précédent et que je réitère
Deux vecteurs et
sont colinéaires si et seulement si, il existe un réel
tel que
ou
.
À quoi correspond « ils » ? aux vecteurs, alors c'est non.
En revanche, si vous vouliez dire que les droites (MN) et (BC) sont parallèles, alors d'accord.
Si on veut remonter un peu le temps, vous montrez que, on est bien dans une configuration de la réciproque de Thalès
Donc avec la réciproque de thalès on peut demontrer que MN BC colinéaire et que MN BC sont parallèles : c est sa ?
Ce n'est pas le but de l'exercice. Je vous ai indiqué cela pour montrer ce que l'on voulait faire avec les vecteurs.
D'abord montrer que les vecteurs et
étaient colinéaires pour ensuite en déduire que les droites sont parallèles.
Vous avez maintenant un nouvel outil pour montrer que trois points sont alignés ou que des droites sont parallèles : la colinéarité de vecteurs.


