Inscription / Connexion Nouveau Sujet
produit scalaire &barycentre
Bonjour ,pouvez vous m'aider ds cette question qui m'a bloqué
soit (o,i,j) un RON
soit IGC un triangle isocéle et rectangle en I tel que IC=3
Soient A et B deux points differents du plan tels que G est le barycentre du systeme des pts ponderes {(A,4),(B,1),(C,-2)} et le vecteur AG = 2/3 le vecteur CI
a) determiner vecteur AB en fonction des vecteurs AG et AC
b) montrer que I est le milieu de [AB]
c) montrer que AI = \/13 (racine de 13)
les deux questions a et b sont simples ms c je n'ai pas arrive a repondre
svp donnez moi un truc
ms c je n'ai pas arrive a repondre
mais je ne suis pas arrivé à répondre.
G barycentre de {(A,4),(B,1),(C,-2)} se traduit par 4GA+GB-2GC = 0 (en vecteurs)
as-tu pensé à utiliser cette égalité ?
en décomposant AB avec Chasles tu devrais y arriver.
Bonjour,
c) une petite figure te montrerait que le triangle AGI ... (le prouvre formellement)
et on connait les mesures de IG et AG ...
nota : je me demande bien à quoi sert le "RON" (éviter les sigles ésotériques) là dedans vu que tout est fait par des relations vectorielles qui ne font nulle part intervenir ce repère ...
surtout que sans précisions supplémentaires C est absolument n'importe où sur le cercle de centre I et de rayon 3 ... donc impossible d'avoir les coordonnées de quoi que ce soit autrement que de façon absolument littérales selon le point C choisi et le sens de GIC choisi, qui n'ont absolument aucune importance pour les résultats demandés
ms c je n'ai pas arrive a repondre
lire :
mais la question c, je ne suis pas arrivé à y répondre

(sous entendu j'ai fait les questions a et b)
lake (bonjour),
oui certes, mais :
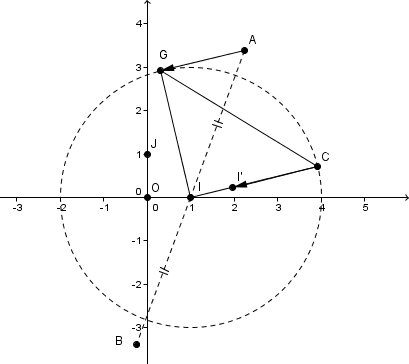
absolument rien dans l'énoncé ne dit que C serai sur un des axes ou quoi.
ha oui javais zapé "la question c" tellement c'était mal écris.
Donc tu veux AI ? Peut-être en commençant par décomposer AI = AG + GI
Je m'excuse pour les fautes de langue que je commets . J'ai une remarque à propos du point I c'est un point du plan non défini .
dans cet exo, "I" est traditionnellement le point unité en abscisse du repère, vu que on commence par mettre un repère (O, i, j) sur le plan avant même de parler du triangle
mais comme ce repère est totalement inutile, on peut tout à fait le retirer et alors IGC est effectivement un triangle rectangle isocèle en I, de côté IC = 3, (3 unités quelles qu'elles soient) mis effectivement n'importe où dans le plan (un point I quelconque du plan) avec n'importe quelle orientation, le problème ne dépend pas de la position de ce triangle.



