Inscription / Connexion Nouveau Sujet
Produit scalaire carré
Bonjour à tous,
j'aimerais avoir de l'aide pour cet exercice, je n'arrives pas à commencer, voici l'énoncé :
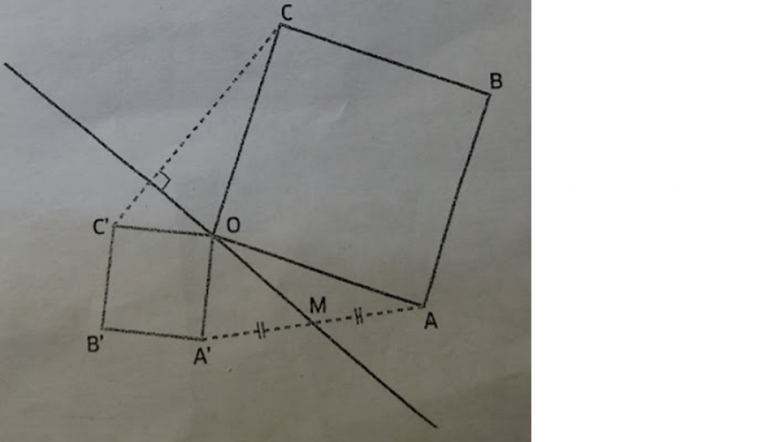
OABC et OA'B'C' sont des carrés.
1) Démontrer que la médiane issue de O dans le triangle AOA' est la hauteur issue de O dans le triangle COC'.
2) Que peut-on dire de la médiane issue de O dans le triangle COC' ?
Je penses que je devrai utiliser le produit scalaire, mais je ne vois pas comment.
Merci de votre aide.
Bonjour,
Essaye de déterminer les coordonnées de A, de C, de A' et de C' dans le repère (DA, DC).
Tu peux appeler R le côté du grand carré et r le côté du petit carré.
Tu peux également appeler  l'angle (DA, DA').
l'angle (DA, DA').
Tu détermineras les coordonnés de M milieu du segment AA'.
Ensuite tu calculeras le produit scalaire vecteur(DM)*vecteur(C'C).
Si tout se passe bien, tu trouveras zéro.
Attention, j'ai appelé D le point O. Il faut donc remplacer dans mon blabla la lettre D par la lettre O. Ça ne change rien au raisonnement.
Bonjour,
Je ne comprend pas comment je censé trouver des coordonnées pour c' et a'
Si quelqu'un veux bien m'aider, merci
Bonjour,
"des coordonnées" que de complications ...
décomposer avec Chasles OM et CC'
et le développement du produit scalaire donne la réponse en deux lignes.
sans "R, r, theta" etc totalement inutiles.
indice : (en vecteurs bien sur ! )
OM = OA + AM
OM = OA' + A'M
additionner et AM + A'M = ?


