Inscription / Connexion Nouveau Sujet
Produits scalaires dans un carré
ABCD est un carré de côté 1. On construit les points E et F tels que :
CE= 3/2 CD et BF= 3/2 BC (vecteurs)
Démontrer que les droites (AF) et (BE) sont perpendiculaires :
1) par calcul vectoriel.
2) En se plaçant dans le repère orthonormé (B;C;A)
Si qqn à des idées.. Merci
Bonjour, je suis en difficultés sur un exercice de produits scalaires, je pige rien..
ABCD est un carré de côté 1. On construit les points E et F tels que :
CE= 3/2 CD et BF= 3/2 BC (vecteurs)
Démontrer que les droites (AF) et (BE) sont perpendiculaires :
1) par calcul vectoriel.
2) En se plaçant dans le repère orthonormé (B;C;A)
Si qqn a des idées..
Bonjour, je suis en 1ere et j'ai un DNS à faire pour la rentrée.
Ce dernier est presque finit, mais je pêche sur un exercice..
ABCD est un carré de côté 1. On construit les points E et F tels que :
vecteur CE = 3/2 du vecteur CD et vecteur BF = 3/2 du vecteur BC
¤ Démontrer que les droites (AF) et (BE) sont perpendiculaires :
1) Par des calculs vectoriels.
2) Avec le repère orthonormé (B;C;A)
*** message déplacé ***
OK. Alors, la première chose à faire : une figure. Commence par dessiner un carré, pas trop grand. Puis, pour placer le point E, c'est facile : on te dit que CE = 3/2 CD (je mets les vecteurs en gras). Ca veut dire 2 choses : 1, que les points C, D et E sont alignés dans cet ordre ; 2, que la longueur du segment CE vaut 1,5 fois celle du segment CD.
Tu prolonges donc le coté CD dans le sens C -> D d'une demi unité de longueur, et tu obtiens le point C.
Meme construction pour obtenir le point F, qui se trouve aligné aveec B et C et tel que C est entre B et F.
Pour la question 1, on écrit AF = AB +BF et BE = BC + CE (tout ça en vecteurs). Fais alors le produit scalaire de AF par BE et tu obtiendras 4 termes dont deux sont nuls (AB.BC et CE.BF, car vecteurs perpendiculaires), et les deux autres sont égaux et opposés. Donc AF.BE = 0 entraine AF  BE.
BE.
On verra ensuite pour la question 2.
Prbebo.
Bonjour Liju02,
si tu as lu ma réponse à jouly14, alors fais comme je l'ai expliqué : quand la figure sera faite, le reste ira tout seul.
Prbebo.
bonjour
1) AF=AB+BF=AB+(3/2)BC ; en vecteurs
BE=BC+CE=BC+(3/2)CD=(-3/2)AB+BC ; car CD=-AB
donc
AF.BE=(AB+(3/2)BC).((-3/2)AB+BC)=(-3/2)AB²+AB.BC+(-9/4)BC.AB+(3/2)BC²
=(-3/2)+(3/2) ; car AB²=1 et BC²=1 et AB.BC=0
=0
donc
(AF) perpendiculaire à (BE)
2) (B;C;A) repère prthonormée direct
dans ce repère:
C(1;0)
A(0;1)
E(1;3/2)
F(3/2;0)
AF(xF-xA;yF-yA)=(3/2;-1)
BE(1;3/2)
donc
AF.BE=(3/2)(1)+(-1)(3/2)=3/2-3/2=0
*** message déplacé ***
Merci Prbebo pour la question 1, tu expliques trop bien 
Tu as du tps pour m'expliquer la deuxieme façon de faire ?
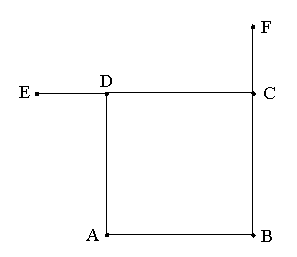
Avec plaisir. Pour ca il faut que je raisonne sur une figure, aussi regarde celle que j'ai faite ci-dessous. Il est possible qu'elle ne soit pas comem la tienne, ca depend comment on place les points A, B, C et D sur le carre.
De meme, la phrase de ton enonce "le repère orthonormé (B;C;A)" est ambigue car elle ne dit pas ou est l'origine du repere, ni comment sont les deux axes. Aussi je vais choisir mon repere moi-meme, tu n'auras qu'a adapter mon corrige au repere demande dans ton exercice, car de toutes facons les calculs sont vraiment identiques.
Je vais donc choisir comme repere les cotes AB et AD, donc il a pour origine A, pour axe des abscisses AB, et pour axe des ordonnees AD.
Marche a suivre : pour montrer que les droites BE et AF sont perpendiculaires, il faut exprimer les coordonnees des vecteurs BE et AF dans le repere choisi, puis faire leur produit scalcaire : si ce produit est nul, c'est gagne.
Coordonnees des points :
A(0;0) ; B (1;0) ; E(-1/2;1) ; F(1;3/2).
Coordonnees des vecteurs :
BE = AE - AB = (-3/2;1) ; AF = (1;3/2).
Il faut que tu revises comment on calcule un produit scalaire quand les vecteurs sont projetes sur une base orthonormale : c'est xx' + yy', ou x et y sont les coordonnees du premier vecteur, x' et y' celles du second.
Si tu calcules BE.AF avec les coordonnees trouvees ci-dessus, tu vas obtenir 0 : donc les deux vecteurs sont bien perpendiculaires.
J'ai change d'ordi depuis tout a l'heure et je suis ici avec un clavier americain, c'est pourquoi il n'y a plus d'accentuation dans mes messages.
Si tu as des questions n'hesite pas.
Prbebo.