Niveau première

regle du parallelogramme et produit scalaire

Posté par
hcen009 15-10-11 à 21:25

Bonsoir
j'ai besoin de votre aide s'il vous plait
1. a. Montrer en utilisant la règle du parallélogramme que

|| $\vec{u}$ + $\vec{v}$ ||²-|| $\vec{u}$ - $\vec{v}$ ||²=4( $\vec{u}$ . $\vec{v}$ ).

b. utiliser la règle du parallélogramme pour montrer que:
8( $\vec{u}$ . $\vec{v}$ + $\vec{u}$ . $\vec{w}$ )= 2(|| $\vec{v}$ + $\vec{u}$ ||²+|| $\vec{w}$ + $\vec{u}$ ||²)-2(|| $\vec{v}$ - $\vec{u}$ ||²+|| $\vec{w}$ - $\vec{u}$ ||²

2)utiliser la règle du parallélogramme pour montrer que:
8( $\vec{u}$ . $\vec{v}$ + $\vec{u}$ . $\vec{w}$ )=(|| $\vec{v}$ + $\vec{w}$ +2 $\vec{u}$ ||²+|| $\vec{v}$ - $\vec{w}$ ||²)-(|| $\vec{v}$ + $\vec{w}$ -2 $\vec{u}$ ||²+||
$\vec{v}$ - $\vec{w}$ ||²)

3. en déduire que u.(v+w) = u.v + u.w (en vecteur)

mon travail
pour la question 1. j'ai fais:
on sait que :
|| $\vec{u}$ + $\vec{v}$ ||²=|| $\vec{u}$ ||²+|| $\vec{v}$ ||²+2( $\vec{u}$ . $\vec{v}$ ).(1)

|| $\vec{u}$ - $\vec{v}$ ||²=|| $\vec{u}$ ||²+|| $\vec{v}$ ||²-2( $\vec{u}$ . $\vec{v}$ ).(2)
en soustrayant (1)et (2) on obtient

|| $\vec{u}$ + $\vec{v}$ ||²-|| $\vec{u}$ - $\vec{v}$ ||²=4( $\vec{u}$ . $\vec{v}$ ).
b.d'apres 1.a.
|| $\vec{u}$ + $\vec{v}$ ||²-|| $\vec{u}$ - $\vec{v}$ ||²=4( $\vec{u}$ . $\vec{v}$ ).

|| $\vec{u}$ + $\vec{w}$ ||²-|| $\vec{u}$ - $\vec{w}$ ||²=4( $\vec{u}$ . $\vec{w}$ ).
en multipliant par 2 et en additionnant les 2 égalites on obtient le resultat

pour la question 2) je ne sais pas comment faire c'est compliqué. et comment en déduire que u.(v+w) = u.v + u.w ?

merci beaucoup d'avance

Posté par re : regle du parallelogramme et produit scalaire 15-10-11 à 21:32

c'est très bien, mais c'est quoi, pour toi, la règle du parallélogramme ?

parce que ton exercice te demande de montrer une relation ( u(v+w) = uv+uw )à partir d'une autre relation et celle que tu utilises ( (u+v)²=u²+2uv+v² ) est une conséquence de celle que tu dois démontrer, alors ça se mord un peu la queue...

Posté par re : regle du parallelogramme et produit scalaire 15-10-11 à 21:40

Bonsoir dhalte
oui le but de l'exercice et de montrer la relation
u.(v+w) = u.v + u.w
mais je ne comprends pas comment montrer la question 2

Posté par re : regle du parallelogramme et produit scalaire 15-10-11 à 21:54

et tu n'as pas répondu à ma question.

Posté par re : regle du parallelogramme et produit scalaire Posté le 15-10 15-10-11 à 22:15

on a vu dans le cours produit scalaire et identités remarquables
(u+v)²=u²+2uv+v²
(u-v)²=u²-2uv+v²
(u+v)²-(u-v)²=4u.v
(u+v)²+(u-v)²=2u²+2v²
je crois la règle du parallélogramme c'est l'une des relations ci-dessus

Posté par re : regle du parallelogramme et produit scalaire 16-10-11 à 01:00

l'exercice qui t'est demandé est très théorique, et je ne suis pas certain qu'il te soit très profitable.

la règle du parallélogramme s'énonce ainsi :
dans un parallélogramme, la somme des carrés des longueurs des cotés est égale à la somme des carrés des longueurs des diagonales.

Cette propriété est caractéristique des parallélogrammes, à savoir que si un quadrilatère la vérifie, alors c'est un parallélogramme.

Maintenant, quand on veut traduire cela en termes de vecteurs, on rappelle d'abord quelques propriétés
Soient A et B deux points et $\vec u=\vec{AB}$ , alors le carré de la distance AB est aussi le carré de la norme du vecteur $\vec u$
$||\vec u||^2=AB^2$

si ABCD est un parallélogramme, alors soit
$\vec u=\vec{AB} \\ \vec v = \vec{AD}$
$\vec u+\vec v = \vec{AC}$ est la première diagonale
$\vec u-\vec v = \vec{DB}$ est la seconde diagonale
$2||\vec u||^2+2||\vec v||^2$ est la somme des carrés des longueurs des cotés
$||\vec u+\vec v||^2+||\vec u-\vec v||^2$ est la somme des carrés des longueurs des diagonales

donc la règle du parallélogramme devient, en termes de vecteurs
$2||\vec u||^2+2||\vec v||^2=||\vec u+\vec v||^2+||\vec u-\vec v||^2$

toi, tu pars d'une toute autre relation, à savoir
$||\vec u+\vec v||^2 = ||\vec u||^2+||\vec v||^2+2\vec u.\vec v$
et en changeant $\vec v$ en $-\vec v$ (et en admettant la symétrie du produit scalaire)
$||\vec u-\vec v||^2 = ||\vec u||^2+||\vec v||^2-2\vec u.\vec v$

donc déjà ces deux dernières relations ne sont pas directement l'expression de la règle du parallélogramme couramment admise en géométrie élémentaire.

mais admettons

alors tu as montré que
$||\vec u+\vec v||^2 - ||\vec u-\vec v||^2 = 4\vec u.\vec v$

à partir de là, l'exercice veut te faire établir une relation dite de linéarité vérifiée par le produit scalaire, à savoir $\vec u.(\vec v+\vec w) = \vec u.\vec v + \vec u.\vec w$

Evidemment, on doit s'interdire toute utilisation d'une règle avancée qui en fait serait une conséquence de celle qu'on veut montrer. D'où la complexité des manipulations qui vont suivre.

à partir de l'expression ci-dessous, on va établir de nouvelles relations :
$||2\vec u+(\vec v+\vec w)||^2 - ||2\vec u-(\vec v+\vec w)||^2$

on utilise la relation déjà vue :
$||\vec u+\vec v||^2 - ||\vec u-\vec v||^2 = 4\vec u.\vec v$
où on remplace $\vec u$ par $2\vec u$ et $\vec v$ par $\vec v+\vec w$

donc
$||2\vec u+(\vec v+\vec w)||^2 - ||2\vec u-(\vec v+\vec w)||^2 = 4\times(2\vec u).(\vec v+\vec w)$

c'est une simple manipulation de substitution.

et une règle non dite : la linéarité par rapport au scalaire, à savoir la relation $4\times(2\vec u)=8\vec u$

ce qui permet d'établir que
$||2\vec u+(\vec v+\vec w)||^2 - ||2\vec u-(\vec v+\vec w)||^2 = 8\vec u.(\vec v+\vec w)$

la seconde manipulation est plus exotique, il va falloir s'accrocher
on va écrire cela
$||2\vec u+(\vec v+\vec w)||^2=||(\vec u+\vec v)+(\vec u+\vec w)||^2$
$||2\vec u-(\vec v+\vec w)||^2=||(\vec u-\vec v)+(\vec u-\vec w)||^2$
et on développe laborieusement les deux expressions à l'aide de la relation $||\vec u+\vec v||^2 = ||\vec u||^2+||\vec v||^2+2\vec u.\vec v$

$||(\vec u+\vec v)+(\vec u+\vec w)||^2=||\vec u+\vec v||^2+||\vec u+\vec w||^2+2(\vec u+\vec v).(\vec u+\vec w)$
$||(\vec u-\vec v)+(\vec u-\vec w)||^2=||\vec u-\vec v||^2+||\vec u-\vec w||^2+2(\vec u-\vec v).(\vec u-\vec w)$

et on continue le développement
$||(\vec u+\vec v)+(\vec u+\vec w)||^2=||\vec u||^2+||\vec v||^2+2\vec u.\vec v+||\vec u||^2+||\vec w||^2+2\vec u.\vec w+2(\vec u+\vec v).(\vec u+\vec w)$
$||(\vec u-\vec v)+(\vec u-\vec w)||^2=||\vec u||^2+||\vec v||^2-2\vec u.\vec v+||\vec u||^2+||\vec w||^2-2\vec u.\vec w+2(\vec u-\vec v).(\vec u-\vec w)$

et on soustrait les deux expressions, ce qui fait disparaître quelques termes
$||(\vec u+\vec v)+(\vec u+\vec w)||^2-||(\vec u-\vec v)+(\vec u-\vec w)||^2=4\vec u.\vec v+4\vec u.\vec w+2(\vec u+\vec v).(\vec u+\vec w)-2(\vec u-\vec v).(\vec u-\vec w)$

donc jusque là, on a établi que :
$8\vec u.(\vec v+\vec w)=4\vec u.\vec v+4\vec u.\vec w+2(\vec u+\vec v).(\vec u+\vec w)-2(\vec u-\vec v).(\vec u-\vec w)$

or nous avons, grâce à la relation $||\vec u+\vec v||^2 - ||\vec u-\vec v||^2 = 4\vec u.\vec v$ , les relations suivantes :
$4(\vec u+\vec v).(\vec u+\vec w) = ||(\vec u+\vec v)+(\vec u+\vec w)||^2 - ||(\vec u+\vec v)-(\vec u+\vec w)||^2$
simplifions
$4(\vec u+\vec v).(\vec u+\vec w) = ||2\vec u+\vec v + \vec w||^2 - ||\vec v-\vec w||^2$

de la même manière
$4(\vec u-\vec v).(\vec u-\vec w) = ||2\vec u-(\vec v + \vec w)||^2 - ||-(\vec v-\vec w)||^2$

avec encore une règle non dite : $||-v||=||\vec v||$

$4(\vec u-\vec v).(\vec u-\vec w) = ||2\vec u-(\vec v + \vec w)||^2 - ||\vec v-\vec w||^2$

donc la quantité précédente $2(\vec u+\vec v).(\vec u+\vec w)-2(\vec u-\vec v).(\vec u-\vec w)$ devient
$2(\vec u+\vec v).(\vec u+\vec w)-2(\vec u-\vec v).(\vec u-\vec w)=\frac12(||2\vec u+\vec v + \vec w||^2-||2\vec u-(\vec v + \vec w)||^2)$

c'est à dire
$2(\vec u+\vec v).(\vec u+\vec w)-2(\vec u-\vec v).(\vec u-\vec w)=\frac12(8\vec u.(\vec v+\vec w))=4\vec u.(\vec v+\vec w)$

alors on revient à
$8\vec u.(\vec v+\vec w)=4\vec u.\vec v+4\vec u.\vec w+2(\vec u+\vec v).(\vec u+\vec w)-2(\vec u-\vec v).(\vec u-\vec w)$

qui devient
$8\vec u.(\vec v+\vec w)=4\vec u.\vec v+4\vec u.\vec w+4\vec u.(\vec v+\vec w)$

ce qui se simplifie en
$\vec u.(\vec v+\vec w)=\vec u.\vec v+\vec u.\vec w$

ouais... on a vu exercices moins abscons pour une classe de première.

Posté par re : regle du parallelogramme et produit scalaire 16-10-11 à 01:40

Bravo dhalte tu as bien expliqué l'exercice difficile ,merci j'ai bien compris

Posté par re : regle du parallelogramme et produit scalaire 16-10-11 à 07:40

dernier raffinement

donc la règle du parallélogramme devient, en termes de vecteurs
$2||\vec u||^2+2||\vec v||^2=||\vec u+\vec v||^2+||\vec u-\vec v||^2$

toi, tu pars d'une toute autre relation, à savoir
$||\vec u+\vec v||^2 = ||\vec u||^2+||\vec v||^2+2\vec u.\vec v$

la relation entre les deux : le théorème d'Al-Kashi
dans tout triangle ABC de trois points distincts, tel que AB=c, BC=a, CA=b, $\theta=\widehat{BAC}$
on a $a^2=b^2+c^2-2bc\cos(\theta)$
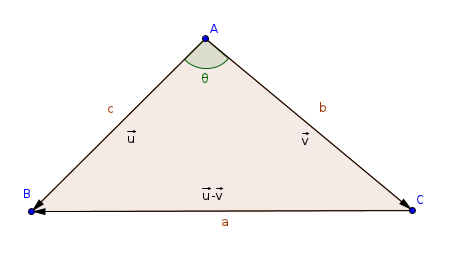
regle du parallelogramme et produit scalaire
or le produit scalaire tel que présenté en lycée est défini par
$\vec u.\vec v = ||\vec u||\times||\vec v||\times\cos(\widehat{\vec u,\vec v})$

si on pose
$\vec u=\vec{AB} \\ \vec v=\vec{AC}$

alors on a $\vec u-\vec v=\vec{CB}$ et donc $||\vec u-\vec v||^2=||\vec{CB}||^2=a^2$
et $\widehat{BAC} = \widehat{\vec u,\vec v}$

et $a^2=b^2+c^2-2bc\cos(\theta)$ devient
$||\vec u-\vec v||^2=||\vec v||^2+||\vec u||^2-2||\vec v||\times||\vec u||\times\frac{\vec u.\vec v}{||\vec u||\times||\vec v||}$

et après simplification on obtient
$||\vec u-\vec v||^2=||\vec u||^2+||\vec v||^2-2\vec u.\vec v$

En considérant C' symétrique de C par rapport à A, on a
$\vec{AC'}=-\vec{AC}=-\vec v$
$\vec{C'B}=\vec u+\vec v$
$\widehat{BAC'}=\pi-\theta$

et dans le triangle ABC' la relation
$C'B^2=b^2+c^2-2bc\cos(\pi-\theta)=b^2+c^2+2bc\cos(\theta)$

ce qui se traduit en termes de vecteurs par :
$||\vec u+\vec v||^2=||\vec u||^2+||\vec v||^2+2\vec u.\vec v$
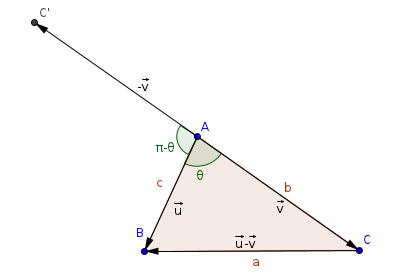
regle du parallelogramme et produit scalaire

et donc en faisant la somme de ces deux relations
$||\vec u-\vec v||^2=||\vec u||^2+||\vec v||^2-2\vec u.\vec v$
$||\vec u+\vec v||^2=||\vec u||^2+||\vec v||^2+2\vec u.\vec v$

on obtient celle de la règle du parallélogramme
$||\vec u+\vec v||^2+||\vec u-\vec v||^2 = 2||\vec u||^2+2||\vec v||^2$

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

Produit scalaire en première
5 fiches de mathématiques sur "Produit scalaire" en première disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

23 visiteurs

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

regle du parallelogramme et produit scalaire

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths