Inscription / Connexion Nouveau Sujet
Relation métrique
7. Relation métrique
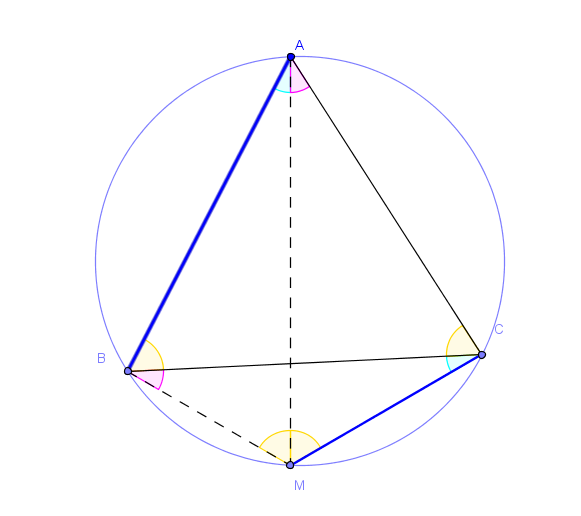
ABC est triangle équilatéral.
M un point du cercle circonscrit (c), M est entre B et C.
Montrer que MA = MB + MC.
Soit I le point de [AM] équidistant de M et C.
MIC triangle isocèle ayant un angle de 60° (angle inscrit AMC dans le cercle (c) égal l'angle ABC), est aussi équilatéral.
La rotation de centre C et d'angle 60° transforme I en M et A en B.
Donc IA = MB et MB + MC = IA + IM = MA.
Merci de m'aider a trouver une autre méthode en utilisant seulement les angles inscrits et les triangles semblables
Bonjour,
Pourquoi veux-tu une autre méthode en utilisant seulement les angles inscrits et les triangles semblables ?
Bonjour,
si on tient vraiment à ne pas utiliser les rotations, on peut passer par en réalité une démonstration du théorème de Ptolémée ... (par les triangles semblables cette démonstration)
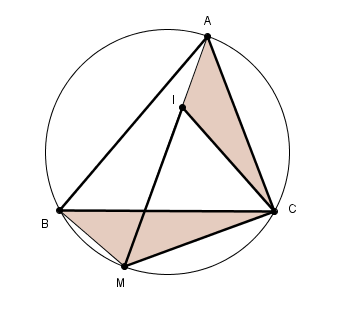
considérons donc 4 points ABCM d'un cercle
construisons le triangle MCI (directement) semblable au triangle BCA
MI/AB = MC/BC et donc MI.BC = AB.MC
justifier que I est sur MA et que les triangles BCM et ACI sont alors semblables (angles inscrits et somme des angles d'un triangle etc)
on tire AI/BM = AC/BC soit AI.BC = BM.AC
en ajoutant ces relations membre à membre on obtient
(MI+AI)BC = AB.MC + BM.AC et donc le théorème de Ptolémée :
AM.BC = AB.MC + AC.MB
si ABC est équilatéral AB = AC = BC cela donne directement et instantanément la relation demandée dans l'exo, qui est ainsi un simple corollaire du théorème de Ptolémée ...
ton triangle MCI est la même chose que mon triangle MCI
(moi dans le cas général du théorème de Ptolémée, toi dans le cas particulier du triangle ABC équilatéral)
mais pourquoi faire aussi compliqué quand on a déja une démonstration simple ...
Merci Mr mathafou 
mais pourquoi faire aussi compliqué quand on a déja une démonstration simple ...
tous simplement parce que la rotation est en dehors du cours


a ce compte là les triangles semblables non plus (du moins en France avec les programmes actuels)
en prenant ton cas particulier de triangle équilatéral, il n'y a pas vraiment besoin de rotations pour exprimer que tes triangles IBC et MBC sont non seulement semblables mais isométriques (angles égaux comme pour ma démonstration de Ptolémée, et côté AC = BC)


