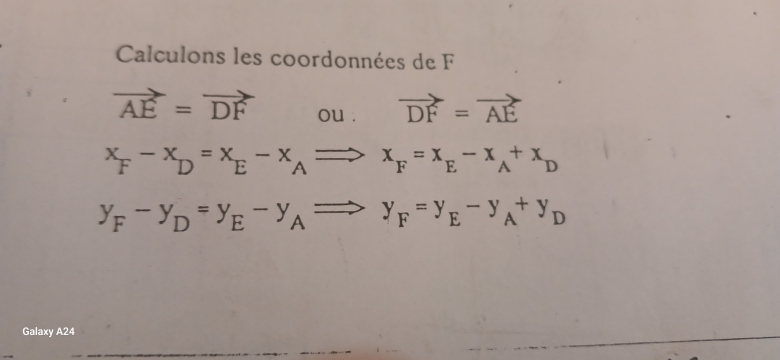Inscription / Connexion Nouveau Sujet
repère
bonjour à tous j'ai besion d'aide
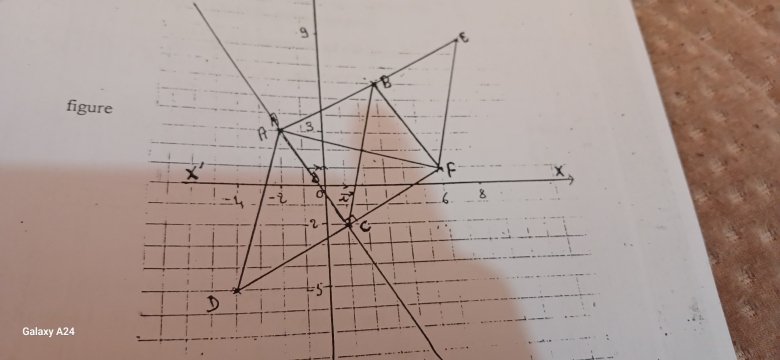
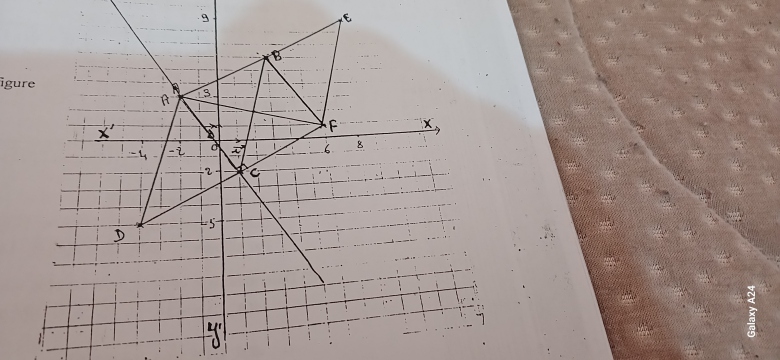
dans un repère muni d'un repère orthonormé (o;i;j) on considère les point A(-2;3);B(3;6);C(1;2);D(-4;5) montre que les bipoint (A;B) et(C;D)sont équippolents en deduire nature
calcule les coordonné du point e tel que B milieu du bipoint (A;E)
calcule les coordonné de F le quadrilateur A;E;F;D soit un parallelogramme
montre que le les draite (A;C) et (D;F) sont perpendiculaire
compare les distance A à C et C à F
vérifie ton énoncé, stp..
A(-2;3) ; B(3;6) ; C(1;2) ; D(-4;5) : tu es sûr ?
"en deduire nature" il manque la fin de la phrase...
bonjour
effectivement il ya une erreur
les coordonnée du point D(-4;-5) et du pointC(1;-2)
le reste de la phrase c'est endeduire la nature du quadrupplet
Bonjour,
tu devais répondre dans ton autre post.
Je te laisse avec Leile que je salue
*** message déplacé ***
OK, pour ta figure.
q1)
"montre que les bipoint (A;B) et(C;D)sont équippolents"
je pense que c'est plutôt "montre que les bipoint (A;B) et (D, C)sont équippolents "
tu sais comment faire ?
les bipoints (A, B) et (D, C) sont équippolents si les segments AC et BD ont même milieux.
tu sais calculer les coordonnées du milieu de [AB], n'est ce pas ?
voyons EAGLEBIRD19, si tu sais le faire, fais le !!
ne m'attends pas, avance !
calcule les coordonnées du milieu de AC,
calcule celles du milieu de BD,
si tu tombes sur les mêmes coordonnées, c'est que AC et BD ont même milieu.
que peux tu en conclure pour le quadrilatère ABCD ?
c'est ça.
milieu de AC (-1/2 ; 1/2)
milieu de BD (-1/2 ; 1/2)
AC et BD ont même milieu : un quadrilatère dont les diagonales se coupent en leurs milieux est un parallélogramme, donc ABCD est un parallélogramme.
question suivante :
calcule les coordonnées du point E tel que B milieu du bipoint (A;E)
fais le calcul, vérifie ton résultat sur ta figure.
vas y !!
OK pour E(8,9) 
question suivante :
pour que AEFD soit un parallélogramme, il suffit que ses diagonales ED et AF se coupent en leur milieux.
calcule les coordonnées du milieu de ED (appelle le par exemple K)
et ensuite, calcule celle de F, telles que K soit le milieu de AF.
à toi !
EAGLEBIRD19,
je ne comprends pas :
les formules que tu me donnes ne correspondent pas au calcul du milieu d'un segment..
et pour la suite, on dirait plutôt un corrigé que tu aurais eu par ailleurs.
Quel est ton travail au juste ?
EAGLEBIRD19,
je ne comprends pas :
les formules que tu me donnes ne correspondent pas au calcul du milieu d'un segment..
alors comment as tu calculé les coordonnées du milieu de AC ? et celles de E ? montre tes calculs et non pas seulement une formule...
et pour la suite, on dirait plutôt un corrigé que tu aurais eu par ailleurs.
Quel est ton travail , ce que tu as réellement fait, au juste ?