bonsoir


d'après le cours, que peux-tu déduire de cette information  : [i]" f admet un maximum local en 1"[/i ?

Bonjour,

carita petite erreur d'énoncé il manque un b

je te laisse avecLina7533

f(x) = ax^3 + 2x^2 + cx + d  ---- il n'y a pas de b ?

normalement b veut 2 daprès l'énoncé

bonsoir Pirho
oui, j'ai vu ça quand j'ai commencé la résolution.

c'est à dire que la f(1) est la plus grande valeur de la fonction f

Lina7533
notre question était plutôt : est-ce 2 ou est-ce b sur l'énoncé qui définit l'expression de f ?

la question posée :
" établir un système de 4 équations dont les inconnues sont les nombres réels a, b, c et d."
laisse penser que le bon énoncé est :  f est la fonction polynôme du 3ème degré telle que f(x) = ax^3 + 2x^2 + cx + d

tu peux vérifier, s'il te plait, avant qu'on se lance dans les calculs ? merci

** laisse penser que le bon énoncé est :  f est la fonction polynôme du 3ème degré telle que f(x) = ax^3 + bx^2 + cx + d

on peut pas dire que b vaut 2?

oui je viens de vérifier , je n'ai pas fait d'erreur

je vous avoue que je n'ai jamais fait du 3ème degrés, je ne sais meme pas que veut dire extremus, je vais faire des recherches immédiatement

la recherche d'extremum, tu en as fait aussi sur du second degré, des fonctions rationnelles, etc.

quand tu étudies une fonction, dis moi quelle étape tu déroules d'ordinaire

non je vous assure c'est exactement ce que j'ai écrit

* quelles étapes

on doit trouver les variations de la fonction normalement ?

soit,
je vais voir où mène la résolution avec cette supposition de b=2...

Pirho, si tu trouves, tu peux poursuivre ?

je suis vraiment désolée si je vous dérange , merci infiniment pour votre aide et votre patience

oui on étudie les variations :
donc on calcule la....?
puis on résout....? puis on étudie le signe de la ...?

et le cas échéant on en déduit....?

mais nonLina7533, tu ne me déranges pas du tout.
c'est juste que je souhaiterais être sure de l'énoncé avant de t'embarquer dans des calculs faux.
bon, je planche et je reviens te dire.

on calcule la dérivée , donc on aura une fonction du second degrés, on résout une équation et ensuite on étudie le signe f'
mais je ne sais pas si on a les mêmes formules pour le 3ème degrés

alors, très rapidement, on se rend compte que b=2 n'est pas correct

donc la fonction de départ est bien f(x) = ax^3 + bx^2 + cx + d  

oui
on résout f '(x) = 0  pour trouver les éventuelles racines de la dérivée
puis on étudie le signe de f '(x)

et si le signe change autour d'une racine, c'est que la fonction atteint là un .....?

je pense que mon professeur s'est trompé

un extremum ?

oui, ça arrive
mais tu peux partir sur la fonction que je t'ai donnée,
je te confirme qu'à la fin on retrouve bien toutes les données de l'énoncé.

mais comment peut-on trouver la dérivée si on a ni a ni b ni c ni d?

eh oui ! extremum

donc si " f admet un maximum local en 1, un minimum local en −1 "
ça signifie qu'en 1 et en -1, on a ..........quelles égalités?

mais comment peut-on trouver la dérivée si on a ni a ni b ni c ni d?

et en quoi ça gène ?
on dérive par rapport à x,
a b c et d sont des coefficients que l'on va trimbaler tels quels, comme si c'était des nombres connus.
tu essaies ?

f'(x)=3ax^2+2bx+c
et pour les égalités je n'ai pas réussi

ah on peut dire que f'(-1)=0
et f'(1)=0 aussi ?

f '(x) parfait

et pour les égalités je n'ai pas réussi
admettons que l'on trouve une racine x₁ en résolvant f '(x) = 0  ----- donc f '(x₁) = 0
et que l'étude du signe de f '(x) nous confirme que le signe de f ' change de part et d'autre de x₁.

==> on en déduit qu'en x₁, la fonction atteint un extremum (cf ta réponse de 18h21).

tu vois où je veux en venir par rapport à " f admet un maximum local en 1, un minimum local en −1"?
quelles égalités on peut poser ?

on peut dire que  x1= -1 et x2=1?

hum, oui, 1 et -1 sont les 2 racines de la dérivée (second degré, maxi 2 racines)

mais on te demande de traduire l'énoncé en équations
f '(1) = 0    utilise la dérivée que tu as établie, et remplace ---> tu as ta 1ère équation en a b et c

puis rebelote pour -1

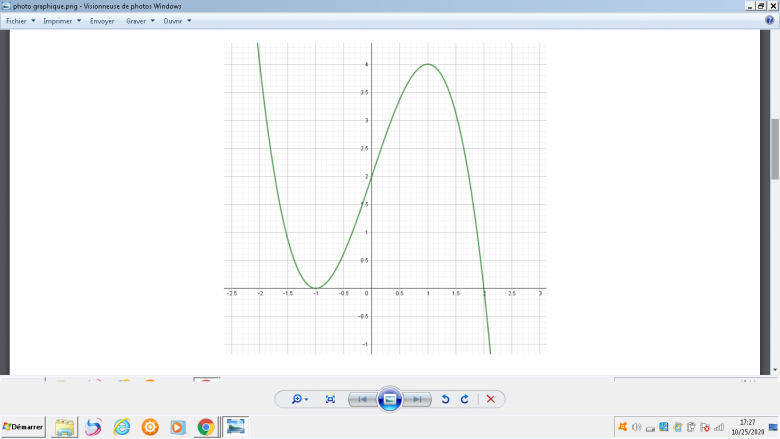
je crois que j'ai trouvé les variations , entre - l'infini et -1 c'est décroissant , ensuiste entre -1 et 1 c'est croissant ensuite entre 1 et +l'infini c'est décroissant

ah donc les variations ne vont pas m'aider

variation : ce que tu dis est juste.
mais ce n'est pas demandé dans l'exo.

as-tu compris mon message de 18h41 ?

on a        0=a x 1^2 + b x 1 + c
                 0=a x (-1)^2 + b x (-1 )+ c

ouii quand j'ai envoyé le message sur les variations, je n'avais pas encore lu votre message

f'(x)=3ax²+2bx+c
d'où
f '(1) = 0    a x 1^2 + b x 1 + c =0  ------- erreur en rouge

f '(-1) = 0 ....?

merci d'utiliser * pour la multiplication, sinon on confond avec la variable x

**
a x 1^2 + b x 1 + c =0  ------- erreurS en rouge

ah oui mince
                 0=3a *1^2 + 2b x 1 + c
                 0=3a*(-1)^2 +2b* (-1 )+ c

voilà
reste à bien simplifier ces écritures  ---- on va pas laisser 1²... d'accord

et tu as tes 2 premières équations du système.

on a donc:
0=3a+2b+c

0=3a-2b+c ( est-ce nécessaire d'écrire 2b=3a+c?)

il est préférable (ou d'usage) d'écrire =0 à la fin

3a+2b+c = 0   (équation1)
3a-2b+c = 0   (équation2)

-----

la courbe Cf passe par A(0 ;2) et B(−1; 0)
quelles équations tu en déduis ?

pour les deux autres équations , on peut utiliser les coordonnées en écrivant
2=a*0^3+b*0^2+c*0+d
0=a*(-1)^3+b*(-1)^2+c*(-1)+d