Inscription / Connexion Nouveau Sujet
Sens de variation
Bonjour,
j'ai la fonction A(x)= et la fonction B(x)= (A(x))².
On me demande de justifier que sur [0;5], c'est deux fonctions ont le même sens de variation.
Est-ce que j'ai raison si j'avance que B(x)=  u avec u=
u avec u= et
 =
= et que puisque
 est strictement positif sur cet intervalle alors les fonctions A et B ont le même sens de variation sur I?
est strictement positif sur cet intervalle alors les fonctions A et B ont le même sens de variation sur I?
Merci pour votre aide!
Bonjour
Cela pourrait se faire si était un nombre réel
Avez-vous étudié le sens de variation des fonctions composées ?
malou edit > balises Ltx rajoutées 
Dans le chapitre Etude de fonctions, j'ai vu les fonctions  u , (1/u), |u|.
u , (1/u), |u|.
Je ne sais pas ce qui est considéré comme des fonctions composées mais j'ai étudié les cas où  u et aussi u+k. Mais dans ce chapitre, je ne trouve rien de spécifique aux puissances.
u et aussi u+k. Mais dans ce chapitre, je ne trouve rien de spécifique aux puissances.
On peut considérer B comme composée de la fonction A suivie de la fonction .
Soient et
deux fonctions telles que
soit définie sur I
si et
ont même sens de variation alors
est croissante sur I
si et
ont des sens de variation contraires alors
est décroissante sur I
Bonjour à vous deux
une autre piste peut-être plus facile pour alexhdmt
1) est-il sûr de ne pas avoir la dérivée de u² dans son cours ?
sinon
2) u²=u*u dont la dérivée est...très facile à trouver comme produit
et comme B(x)= (A(x))²
on dérive et le tour est joué
Je ne faisais que passer. Choisissez ce qui est le plus simple pour alexhdmt

J'ai vu la dérivée de u² mais dans l'exercice on me demande d'abord de justifier que ces deux fonctions ont les mêmes variations puis ensuite on me demande de dérivée B(x).
Bonjour,
on peut de façon plus élémentaire étudier directement le taux de variation de B en fonction de celui de A
rappel : définition de "fonction croissante" (ou décroissante) .
une fonction est croissante (ou décroissante) dans un intervalle E si pour tous nombres a et b de E avec a < b, F(a)< F(b) (ou F(a) > F(b))
ici il est inutile d'écrire explicitement A et B en remplaçant explicitement x par a et b
écrire A(a) et A(b) tels que suffit. et B(a) = A(a)² etc
11: 28
Soient et
deux fonctions telles que
soit définie sur I
1) si et
ont même sens de variation alors
est croissante sur I
2) si et
ont des sens de variation contraires alors
est décroissante sur I
Donc je dois démontrer que v "o" u est croissante pour affirmer que u et v ont le même sens de variation?
alexhdmt, la prochaine fois, merci de mettre tout ton énoncé recopié au mot près, (on nous demande n'a rien d'un véritable énoncé) dès ta demande, et non pas seulement la 1re question
ça nous aidera à savoir dans quelle direction aller
merci

Avez-vous étudié le sens de variation de A ?
On sait que surest croissante
Sur , si A est une fonction croissante alors
est croissante sur cet intervalle
Sur est décroissante alors
est aussi
décroissante sur cet intervalle
donc même sens de variation
les guillemets sur "o" montrent déja que tu ne comprends pas vraiment cette notation et ce qu'est la composition de deux fonctions.
par définition la fonction est la fonction qui à tout x de l'intervalle I fait correspondre u(v(x))
on dit qu'on a "composé" les deux fonctions u et v
ici il s'agira d'appliquer ça à v(x) = A(x) et u(x) = x²
u(v(x)) est l'élévation au carré de u(x) c'est à dire B(x) = u(A(x))
je m'aperçois que j'ai échangé u et v
je remets avec les mêmes notations que hekla :
les guillemets sur "o" montrent déja que tu ne comprends pas vraiment cette notation
par définition la fonction
on dit qu'on a "composé" les deux fonctions u et v
ici il s'agira d'appliquer ça à u(x) = A(x) et v(x) = x²
v(u(x)) est l'élévation au carré de u(x) c'est à dire B(x) = v(A(x))
Note importante :
dans l'exercice on me demande d'abord de justifier que ces deux fonctions ont les mêmes variations puis ensuite on me demande de dérivée B(x).
tu dois donner l'énoncé mot à mot entier dès le départ
ça éviterait à hekla de poser la question
Avez-vous étudié le sens de variation de A ?
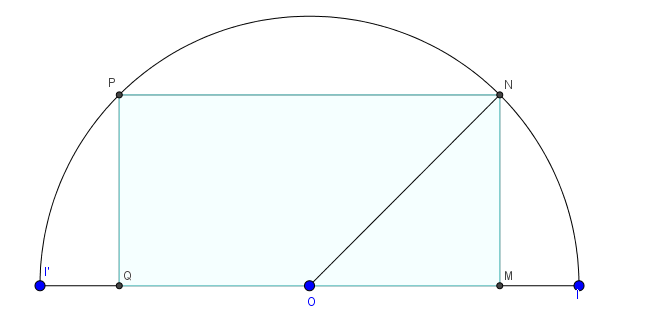
"Sur la figure ci-contre MNPQ est un rectangle inscrit dans le demi-cercle de centre O et de rayon OI=5. On se propose de déterminer la position du point M sur le segment [OI] telle que l'aire du rectangle MNPQ soit maximale.
1. On note x=OM (0 x
x 5) et A(x) l'aire du rectangle MNPQ.
5) et A(x) l'aire du rectangle MNPQ.
a) Démontrer que A(x)=
b) Pour tout nombre réel x de [0;5], on pose B(x)=(A(x))².
Justifier que les fonctions A et B ont le même sens de variation.
2.a) Déterminer la fonction dérivée de la fonction B.
b) Terminer l'étude."
+ Je ne trouve pas ou se situe le symbole "o" pour les fonctions combinés.
Montrer que A et B ont même sens de variation
Si A est croissante sur un intervalle, comme la fonction « carré », notée ici , est croissante sur
alors la composée A suivie de v, c'est-à-dire B, est croissante sur l'intervalle.
De même avec A décroissante.
Pour vous convaincre
On suppose A croissante sur I. Pour tout
À cette inégalité, on applique la fonction qu'on sait être croissante, donc
Conclusion A et B sont alors toutes deux croissantes sur l'intervalle
On fait la même chose avec l'autre cas, toutes les deux décroissantes, on conclut sur le sens de variation de A et B.
La rédaction est incomplète.
On passe alors à la question suivante.
Alors comment puis-je affirme que A est croissante ou décroissante sur un intervalle si je ne l'étudie pas avant? Vraiment je suis perdu je n'ai jamais vu de ma vie les fonctions combinées, je n'ai jamais fait un seul exercice avec. Tout ça pour moi c'est du charabia.
Que vaut B(x) ?
N'est-ce pas un polynôme ? Vous pouvez alors étudier le sens de variation normalement.
On dit composées, pas combinées (simple remarque )
Non, vous cherchez le sens de variation de cette fonction
Dérivée signe de la dérivée sens de variation tableau
Bonjour,
Je modifie les ponctuations pour clarifier le message de hekla :
Là où vous avez montré que B était croissante, vous dites que A l'est.
De même pour décroissante.
Et je corrige une coquille :
Non, vous cherchez le sens de variation de cette fonction

Bonjour
Merci, Sylvieg, pour la surveillance et la correction des erreurs.
Vous avez écrit la définition de B
.
Dans le fil, vous n'avez pas écrit la dérivée, ni le sens de variation, on ne peut donc pas dire que vous avez répondu à la question
2.a) Déterminer la fonction dérivée de la fonction B.
Si à la question 1)b., je dérive la fonction B pour dresser son tableau de variation puis qu'ensuite je fais la même chose avec la fonction A alors automatiquement j'ai déjà répondu à la question 2.
Question 1 b
On vous demande de montrer que A et B ont même sens de variation. C'est tout.
Question 2 a) Déterminer la dérivée de B. C'est donc ici que l'on vous demande de dériver la fonction définie par
2 b) terminer l'étude
signe de la dérivée de B.
sens de variation de B.
tableau pour résumer.
sens de variation de A. Il n'y a rien à ajouter, on reprend le résultat de la question 1
Oui mais la question 1 b, je ne peux pas montrer qu'elles ont le même sens de variation si je ne les dérive pas au préalable pour faire leurs tableaux de variation?
C'est pourtant ce que l'on a fait et il n'y a pas été question de dérivation
On suppose A croissante sur I. Pour tout
À cette inégalité, on applique la fonction qu'on sait être croissante, donc
On a montré que pour tout , tout
Par définition, B est croissante sur I
Conclusion A et B sont alors toutes deux croissantes sur l'intervalle
On fait de même avec l'autre cas, toutes les deux décroissantes,
on conclut : dans les deux cas, le sens de variation de A et B est le même.
je confirme la réponse de hekla
à quelques virgules près car ça c'est faux :
la fonction « carré », notée ici v, est croissante sur [0 ; 5]
la fonction v n'est pas à appliquer sur [0; 5] mais sur l'image par A de [0; 5}
il faut donc montrer que quel que soit x de [0; 5] alors A(x) est > 0 (ou nul) (facile)
A(x) est donc dans [0; +oo[ et la fonction v est bien croissante dans [0 ; +oo[ et la suite de la démo marche.
Je ne vous suis pas, la fonction A est croissante sur [0; 3,536] et décroissante sur [3,536; 5]. Je crois qu'il manque un mot dans votre dernière phrase mais en aucun cas je trouve que v est croissante sur [0;+ [
[
v c'est la fonction carré : x  x² et rien d'autre
x² et rien d'autre
on la limite à [0 +oo[ pour qu'elle soit croissante et que l'on puisse appliquer les calculs qui suivent
et encore et encore, on répète :
on se fiche des variations précises de A et de B pour montrer qu'elles ont les mêmes variations
quelle que soit la fonction A(x), du moment qu'elle est définie et positive partout sur un intervalle (ici sur [0; 5})
les fonctions A(x) et B(x) = A(x)² auront les mêmes variations sur cet intervalle
quelles que soient ces variations
c'est ça qu'on doit démontrer question 1b et rien d'autre.
le problème est que tu ne comprends pas les compositions de fonctions
(déja dit le 16-01-23 à 13:29)
c'est pour ça (parce que la démonstration donnée ici te passe au dessus de la tête, parce que tu ne la comprends pas vraiment) que j'avais suggéré de revenir aux bases, sans utiliser la notion de fonctions composée.
les bases c'est la définition :
f(x) est croissante (respectivement décroissante) dans un intervalle I si quels que soient a et b dans I avec a > b alors f(a) > f(b) (resp. f(a) < f(b))
bref l'étude des variations de f est la même chose que l'étude du signe de f(a) - f(b) selon les valeurs de a et b
appliquons cette définition à l'exo
B(a) - B(b) = A(a)² - A(b)² = (A(a)+A(b))(A(a)-A(b))
or dans tout l'intervalle de définition de A, A(x)  0 (le justifier) et donc A(a)+A(b) > 0
0 (le justifier) et donc A(a)+A(b) > 0
le signe de B(a) -B(b) est donc le même que celui de A(a) -A(b)
et c'est terminé , les variations sont les mêmes quelles que soient ces variations
v étant la fonction « carré », vous avez dû voir en seconde que cette fonction était croissante sur et décroissante sur
Pour tout comme produit de termes positifs
d'où et
donc on est d'accord, mais il vaudrait mieux d'abord donner la valeur exacte.
Il reste à écrire le sens de variation de A
, la fonction A est croissante sur [0; 3,536] et décroissante sur [3,536; 5].
C'est à cela que correspondait ma réponse.