Inscription / Connexion Nouveau Sujet
TD Dichotomie
Bonjour j'ai un td a faire pour la rentrer et je n'arrive pas à faire les questions 3, 4 et 5 et le graphique de l'exercice 2 qui est le suivant :
Soient a et b 2 réels a<b de I tels que f(a)*f(b) <0 (donc 2nomres a et b tels que x0 appartient à I=[a;b]
représentez graphiquement les 2 situations
1) on considère alors c le centre de l'intervalle [a;b] quelle est sa valeur?
2) Trois cas peuvent se présenter :
a) f(c)=0
b) f(c)<0
c)f(c)>0
on suppose que a) ne se produit pas montrer que f(a)*f(c)<0 ou f(b)*f(c)<0
3) Dans un programme on considère alors 3 variables a b et c correspondant au cas précédent, si f(a)*f(c)<0 alors on affecte a b la valeur c sinon on affecte a a la valeur de c. Montrer qu'à la fin de la procédure f(a)*f(b)<0 et a<b
4) On obtient ainsi un intervalle d'amplitude 2* plus petit, la suite des amplitudes des divers intervalles et une suite de quel type ? Quelle est sa limite ?
5) On arrête le processus quand on a atteint la précision souhaitée donc quand l'amplitude b-a est suffisamment petite
Merci de votre aide 
Bonjour,
Ta demande ne semble pas bien clair :
je n'arrive pas à faire les questions 3, 4 et 5 et le graphique de l'exercice 2
C'est quoi l'exercice 2 ?
Le mieux, pour comprendre cette notion de dichotomie, serait encore de faire avec un exemple.
donc 2nomres a et b tels que x0 appartient à I=[a;b]
Qu'est-ce que ce x0 non défini dans l'énoncé ...
Bonjour sur le td il y avait 2 exercices et celui ci est le deuxième
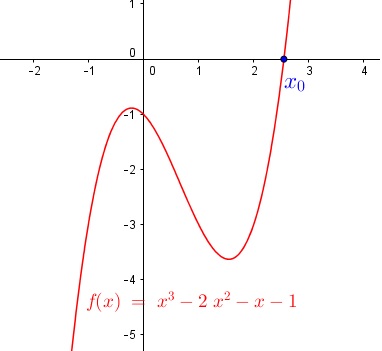
pour x0 il est égal à 0
merci d'avoir répondu 
Non, regarde bien si tu veux être entre 2 et 3, tu es bien obligé de partir de 2 et de rajouter la moitié de l'intervalle.
Oui, c'est cela.
Donc on a f (5/2)=-3/8<0 et f(3)>0
Donc à présent, tu passes sur l'intervalle [5/2,3]
et tu te places à la moitié, soit à x=(5/2) + [3-(5/2)]/2 =11/4
Tu calcules à présent f(11/4) et tu vois si le résultat est positif ou négatif.
Oui, et comme c'est positif, cette fois ci tu abandonnes ta valeur supérieure de ton intervalle, à savoir 3.
Tu passes donc sur l'intervalle [5/2,11/4]=[2,5 ; 2,75], ce qui correspond à un encadrement de x0 tel que :
2,5<x0<2,75
et tu recommences pour avoir plus de précision.
Est-ce compris ?
Oui dans votre exemple je comprends mais des que ce n'est plus précis comme dans l'énoncé je ne comprends pas
Soient a et b 2 réels a<b de I tels que f(a)*f(b) <0
Cela veut dire que f(a) et f(b) sont de signes différents, en d'autres termes qu'ils sont de part et d'autre de l'axe des x. L'un au-dessus, l'autre en dessous.
Si f est strictement croissante entre a et b, alors f(a) sera négatif (en dessous de l'axe des abscisses), et f(b) positif (au-dessus de l'axe des abscisses).
Ce sera l'inverse si f décroissante entre a et b.
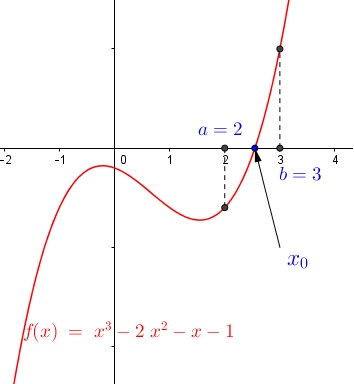
on considère alors c le centre de l'intervalle [a;b] quelle est sa valeur?
Ici, c correspond dans l'exemple que l'on a vu au x en rouge ci-dessous :
Tu te mets à la moitié de l'intervalle, soit à :
Et à présent tu calcules :
Je reprends :
on considère alors c le centre de l'intervalle [a;b] quelle est sa valeur?
Ici, c correspond dans l'exemple que l'on a vu au x en rouge ci-dessous :
Tu te mets à la moitié de l'intervalle, soit à :
Et à présent tu calcules :
Ah oui
Mais pourquoi choisir des nombres précis pourquoi ne pas continuer avec a b et c ?
parce que pour la 3 par exemple les valeurs ne sont pas donnés
Alors tu dois avoir la réponse à ta présente question ==>
Mais pourquoi choisir des nombres précis pourquoi ne pas continuer avec a b et c ?