- Un petit rappel de Cours sur le dénombrement - terminale
- Sept Exercices Q.C.M. sur le dénombrement - terminale
- Complexes, calcul vectoriel, problème - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
Inscription / Connexion Nouveau Sujet
Tracé la courbe d'une fonction
Soit f la fonction définie sur ]0; 1[ par f(x)=x-2+1
Tracer la courbe C de la fonction f
f'(x) =<0 pour tout x appartien de ]0; 1[
Et je trouve le tableau de variation suivant après je ne sai plus comment faire pour tracer la courbe
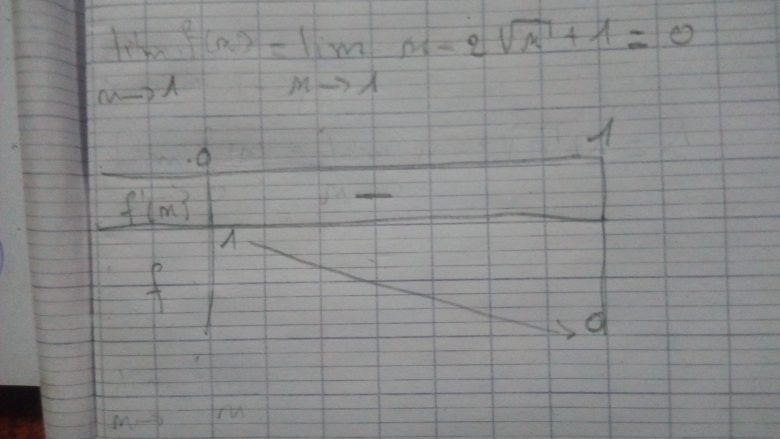
Je cherche les asymptote en -l'infini et à + l'infini
Mais là là fonction est just définie sur ]0; 1]
Malheureusement on n'a pas le droit d'utiliser les calculatrice qui peuvent tracer des fonction c'est strictement interdit
Bonjour,

pour tracer une courbe on trace un certain nombre de points de cette courbe et on les relie
plus on aura de points et plus le tracé sera précis
et c'est tout et point barre.
on peut améliorer le tracé en traçant les tangentes en certains de ces points
salut
1/ tracer la courbe de la fonction racine
2/ tracer son opposé
3/ ajouter 1 <=> .... (traduction géométrique)
4/ élever au carré
autre méthode :
1/ tracer la courbe de la fonction x --> -2 r(x)
2/ tracer la courbe x --> x + 1
3/ "ajouter" les deux
de toute façon il est intéressant de prolonger f(x) sur l'intervalle fermé [0; 1]
rien n'empêche de calculer les points d'abscisses 0 et 1 de cette courbe prolongée !!
quitte à les retirer ensuite de la courbe (ce qui bien entendu ne se voit pas sur un dessin)
ce n'est pas parce que la dérivée n'est pas définie en 0 que la courbe elle même ne l'est pas !
ni qu'on ne peut tracer la tangente en 0 (par une limite) et encore moins en 1.
ça aide à tracer une courbe
pour obtenir des points "à la main" sans calculette, on peut choisir des valeurs de √ x puis en déduite x = (√x)² ...
par exemple si je choisis √x = 0.9 alors x = 0.81 et je peux calculer très facilement l'ordonnée de ce point sans aucune calculette du tout.
etc.
à répéter autant que nécessaire , par exemple entre 0 et 1 par pas de 0.1 ce qui donne 11 points de la courbe en comptant x = 0 et x = 1
ainsi que les tangentes en les extrémités (immédiates).
avec ça le tracé à main levée de la courbe s'en déduit.
est-il possible d'avoir l'enonce en entier ?
On demande une conjecture sur le graphe ?
Soit f la fonction définie sur ]0; 1[ par f(x)=x-2
1.etudier les variation de f
2.demontrer que fof(x)=x
3.Tracer la courbe C de la fonction f (unité graphique 10cm)
Malheureusement on n'a pas le droit d'utiliser les calculatrice qui peuvent tracer des fonction c'est strictement interdit
que le grapheur soit interdit admettons
mais on peut trouver des points à la calculatrice
C'est just qu'on jamais tracer des courbe en cherchant des point
Ont la toujours fait en cherchant les branches infini les asymptote
C'est just qu'on jamais tracer des courbe en cherchant des point
Ont la toujours fait en cherchant les branches infini les asymptote
C'est just qu'on jamais tracer des courbe en cherchant des point
tu n'as jamais rien compris à ce que vous avez toujours fait plutôt, oui.
on ne dit pas d'en chercher, on dit d'en choisir.
une liste arbitraire de points que l'on va reporter sur le repère
la courbe est-elle un quart de cercle ?
d'ailleurs de
on tire
(l'autre partie est
et en développant, le terme en "-2xy" interdit que cela soit un cercle
(dans un exercice cela se prouverait autrement en fait)
c'est en vrai un morceau de parabole dont l'axe est la première bissectrice (la droite y = x)
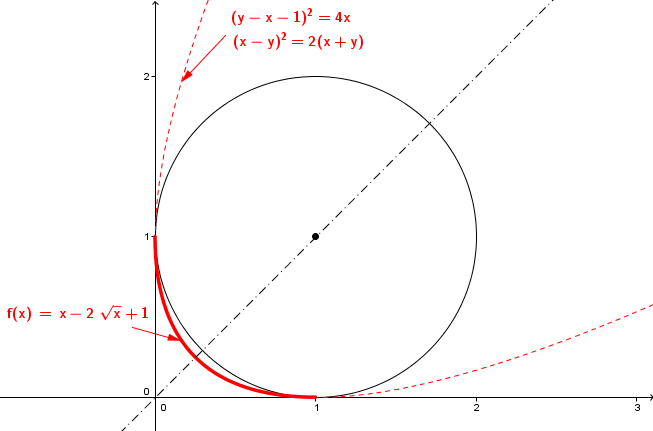
et comme une parabole n'a pas d'asymptote, les histoires d'asymptotes on peut s'assoir dessus !!
je voudrais bien voir d'ailleurs, Mounkaila144, quelles "asymptotes" vous avez bien pu tracer pour tracer la courbe y = x² !!

d'ailleurs c'est général
on trace des asymptotes pour faciliter le tracé d'une courbe quand celle ci en a !
et histoire de les mettre en évidence parce que ce sont une caractéristique très remarquables de certaines courbes, de même que les points à tangente horizontale ou verticale, les points d'inflexion, certaines tangentes etc
mais dans TOUS les cas, asymptotes ou pas, on trace une courbe toujours en traçant un plus ou moins grand nombre de points de la courbe
point barre
d'ailleurs en interne une calculatrice ou un logiciel font exactement pareil !! ils calculent un bon paquet de points isolés de la courbe et les relient par des morceaux lissés (in fine des petits bouts de droite, réduits au pire à un seul pixel de long)
sauf si c'est une droite ou un cercle pour lesquelles on les trace à la règle ou bien au compas (à partir de deux points, si , si !!! si c'est une droite !)
ou avec des algorithme genre Bresenham ou dérivés dans une machine, de nos jours personne ne s'en inquiète vu que c'est fait directement dans la puce graphique de l'ordi !
sauf les concepteurs de puces graphique bien sûr...
je ne vois pas où j'ai répondu aux questions de l'énoncé tel que donné le 12-05-19 à 09:29
à part avoir une idée de la courbe que de toute façon le demandeur refuse de tracer comme on lui dit de le faire, en s'entêtant sur des trucs absurdes d'asymptotes...
je parlais de la nature de la courbe que son prof va peut etre faire en classe.
Du coup Mounkaila144 pourra briller 
il faudrait demontrer en terminale que la courbe n'est pas un arc de cercle.
Pas si simple ?
Peut on prouver la proposition:
si la courbe est un arc de cercle alors le centre de ce cercle est (1;1) ?
on peut démontrer que les tangentes à la courbe en les points d'abscisses 0 et 1 sont ... (en étendant comme j'ai suggéré le domaine de définition à [0;1] au lieu de ]0; 1[)
les propriétés élémentaires des tangentes à un cercle vues en collège montrent alors que le centre du cercle si cercle il y a est sur les perpendiculaires à ces tangentes en leur point de contact, donc en l'intersection de ces perpendiculaires
à condition de les avoir déterminées !
mais déterminer ces tangentes est quasi obligatoire au tracé d'une courbe réaliste :
de même que les points à tangente horizontale ou verticale, les points d'inflexion, certaines tangentes etc
f'(1) est évident
f'(0) est plus compliqué car n'est pas définie !
on peut toutefois trouver la limite de ce f'(x) quand x --> 0 par valeur supérieures
ayant ainsi défini notre arc de cercle candidat, prouver que la courbe n'en est pas un sera d'exhiber une abscisse pour laquelle le point de la courbe est différent du point de même abscisse sur l'arc de cerce (c'est à dire un contre exemple)
n'importe quelle valeur conviendra
pourquoi pas 1/4 (vu que la racine carrée de 1/4 est facile a déterminer sans aucune calculette)
calculer alors la distance au centre du cercle pour vérifier qu'elle est différente du rayon du cercle.
et c'est terminé.
après, le manque flagrant de toute imagination de la part d'élèves auquel on enseigne pendant des années à ne pas penser ... c'est une autre histoire...
il faudrait démontrer en terminale que la courbe n'est pas un arc de cercle.
Pas si simple ?
Peut on prouver la proposition:
si la courbe est un arc de cercle alors le centre de ce cercle est (1;1) ?
si I(m, m) est le centre de ce cercle (hypo.) alors le carré de son rayon hypo. est
or
Dans le plan muni d'un repère (o ; i ; j) on considère les points A(0.5+β; 0) et B(0; 0.5-β) où β est un réel de [-0.5; 0.5]
On note( D) la droite déterminer par les points A et B
1.Determiner une équation D sous le forme a(β)+b(β)+c(β)=0 où a b et c sont trois fonction derivable de la variable β que l'on déterminera
2.soit D' là droite d'équation a'(β)+b'(β)+c'(β)=0 où a' b' et c' désigne les fonctions dérivé respectives et a b et c
a) vérifié que D et D' sont secante en un point N
b) démontré que les coordonnées de N sont N((0.5+β)2; (0.5-β)2)
3. Démontrer que lorsque N décrit [-0.5; 0.5] N décrit la courbe C définie par f(x)=x-2√x+1
4.demontrer que la droite D est tangente en N à la courbe C
D:y=mx+p
m==
p=0.5-β
D :y=x+0.5-β
D :x-y+0.5-β=0
Donc a(β)=
b(β)=1
C(β)=0.5-β
Après je ne sais plus comment déterminer β
*** message déplacé ***
salut
on ne te demande pas de déterminer m (je note m le paramètre) mais de déterminer une équation cartésienne a(m)x + b(m)y + c(m) = 0
*** message déplacé ***
euh...ça a quelque chose à voir avec cet énoncé ? ....![]() Tracé la courbe d'une fonction
Tracé la courbe d'une fonction
tu ne peux pas déterminer 
les quantités a, b et c sont fonctions de 
relis ton énoncé
*** message déplacé ***
euh...ça a quelque chose à voir avec cet énoncé ? ....

relis ton énoncé
Oui c'était la première partie du problème
J'ai cru parvenir à finir le rest moi seul
*** message déplacé ***
D :
Donc j'ai déjà fini par répondre à la question alors
*** message déplacé ***
Mon problème à aussi une partie C
Si je me bloque la dans je fais comment ?
Je peux le poster ici ?
Je veux pas être banni
D :
Donc j'ai déjà fini par répondre à la question alors
*** message déplacé ***
salut
on ne te demande pas de déterminer m (je note m le paramètre) mais de déterminer une équation cartésienne a(m)[b]x + b(m)y + c(m) = 0[/b]
donc on attend ...
2. D':2mx-y-2m=0
a) soit u(0.5+m ; m2-0.25)un vecteur directeur de D
Et u'(1; 2m) un vecteur directeur de D'
u.u'=0.5+m-2m2-0.5m0
Donc D et D'sont secante en N
b) les coordonnées de N
On n'a D:y=x+0.5-m
Et D': y=2mx-2m
Poson x+0.5-m=2mx-2m
=>x=
Jnarrive pas à démontrer les coordonnées de N
Bonjour,
quelle salade.
D: (m-0.5)x-(0.5+m)y+(0.25-m2)=0 OK
D' est obtenue en dérivant par rapport à m chacun des coefficients de D
la dérivée de m-0.5 est 1
celle de (0.5+m) aussi
celle de (0.25-m2) est -2m
donc D' : 1x -1y - 2m = 0
etc...
par ailleurs pour vérifier que les droites ne sont pas parallèles ce n'est pas un produit scalaire qu'il faut faire !!
ton dernier calcul ne rime à rien du tout
manquent des développements et réductions intermédiaires pour résoudre vraiment cette équation en l'inconnue x dont le terme constant est -2m+m = -m et n'apparait nulle part dans x = -m/coefficient de x
mais comme de toute façon ce n'est pas ça l'équation ...
le x que l'on trouve (avec les bonnes équations, et résolue correctement) c'est l'abscisse de N
tu alignes des calculs sans savoir où tu vas ni pourquoi tu les fais ??
et son ordonnée c'est en reportant cette abscisse dans l'équation de l'une des deux droites (bien entendu de la plus simple des deux)
et puis pour trouver l'intersection de deux droites
ax+by+c = 0
a'x+b'y+c' =0
on résout directement ce système tel qu'il est écrit
sans devoir passer par des équations réduites (qui posent problème si le coefficient de x peut s'annuler car il est variable)
2. D':x-y-2m=0
a) soit u(0.5+m ; m2-0.25)un vecteur directeur de D
Et u'(1; 1) un vecteur directeur de D'
det(u ; u')=10
Donc D et D'sont secante en N
2.
(m-0.5)x-(0.5+m)y+(0.25-m2)=0
x-y-2m=0
D=1
Dx=(0.5+m)2
Dy=(0.5-m)2
xN==(0.5+m)2
yN==(0.5-m)2
Dont les résultats à démontrer
Pour les questions 3 et 4 pouvez vous me donnez quelque indice ?
franchement pourquoi faire compliqué quand on peut faire simple :
D a pour équation (2m - 1)x - (2m + 1)y + 0,5 - 2m^2 = 0
D' a pour équation x - y - 2m = 0
a/ on peut le faire avec les vecteurs directeurs et il est évident que les vecteurs u(2m + 1, 2m - 1) et v(1, 1) ne sont pas colinéaires
b/ on donne les coordonnées du point d'intersection N de D et D' ... donc il suffit de vérifier que N appartient à D et D' ... sans avoir besoin de sortir de quelconques formules kabbalistiques ...
3/ revoir l'énoncé ...
il suffit de vérifier que les coordonnées de N vérifient l'équation de C
ou en core que
4/ calculer l'équation de la tangente à C au point d'abscisse N et vérifier qu'on obtient (une équation de) D
OK,
on peut effectivement faire tout ça avec des déterminants.
3. Démontrer que lorsque m (alias β) décrit [-0.5; 0.5] N décrit la courbe C définie par f(x)=x-2√x+1
il suffit de remplacer x de f(x) par l'abscisse de N trouvée question précédente et de voir si ça donne bien l'ordonnée de N
ça prouve que tout point N est bien sur la courbe
pour achever il faut vérifier que toute les abscisses de [0; 1] peuvent être obtenues par un point N avec m ∈ [-0.5; +0.5]
4.demontrer que la droite D est tangente en N à la courbe C
calculer le coefficient directeur de la tangente en N (d'abscisse connue en fonction de m = question 2) et vérifier que c'est celui de D
(inutile d'obtenir l'équation complète de la tangente, l'égalité des coefficient directeurs suffit puisque on sait que ces deux droites passent par N, "par définition")
pour xN = 0 bien entendu la dérivé n'a pas de sens (f(x) n'est pas dérivable en 0)
on peut passer à la limite pour s'assurer que ces deux droites sont alors en fait verticales.
3. Démontrer que lorsque m (alias β) décrit [-0.5; 0.5] N décrit la courbe C définie par f(x)=x-2√x+1
pour achever il faut vérifier que toute les abscisses de [0; 1] peuvent être obtenues par un point N avec m ∈ [-0.5; +0.5]
J'ai pas du tout compris ça
ton écriture initiale "N décrit [-0.5; +0.5]" de toute façon ne veut rigoureusement rien dire du tout car N est un point et pas une valeur qui serait susceptible de parcourir un intervalle de valeurs [-0.5; + 0.5]
la valeur qui varie c'est m, alias β dans l'énoncé d'origine, on a écrit ici partout m parce que c'est plus facile à écrire que β
et on te dit "décrit la courbe" ça ne veut pas dire décrit un morceau de la courbe.
donc il faut bien montrer que quand m décrit l'intervalle [-0.5; +0.5], le point N parcourt toute la courbe définie par f(x) avec x ∈ ]0; 1[ (énoncé de la définition de la courbe C dès le début de l'exo, et pour tout l'exo entier)
donc la démonstration comporte deux phases distinctes
• que pour toute valeur de m , le point N est sur la courbe (mais peut être seulement un morceau seulement de cette courbe)
• que que pour toute position d'un point de la courbe, il existe au moins une valeur de m telle que N soit en ce point là
et les abscisses suffisent pour dire ça car f(x) est une fonction, tout point de la courbe est suffisamment défini par sa seule abscisse, son ordonnée étant alors "automatiquement" f(x)





