Si tu nous donnes la transformation f de la partie A, on pourra te donner notre opinion sur tes résultats.

quoique, tu as déjà donné des résultats qui ne dépendent pas de la partie A.

Alors ton calcul du centre et du rayon : ok.
Alors coordonnées de A et B : ok.

mais quelle est la définition de O ? tu ne la donnes pas.
Habituellement, O est le nom donné à l'origine du repère, le point de coordonnées (0;0).

Ton énoncé dit-il explicitement que O sera le nom donné au centre du cercle ?

Non, on ne me le dis pas, c'est moi qui l'a posée..
Dans la partie A, j'avais IM'=(1/4)IM, c'est une homothétie ce centre I et de rapport 1/4 ...
Merci

Enoncé complet:

Partie A
A et B sont deux points donnés. I est tel que 3AI=AB. A tout point M du plan, on associe M' de la manière suivante:
-N est le milieu de [MB];
-M' est le mileu de [AN]
On dit que M' est l'image de M par une transformation f. On note M'=f(M). Le but de cette partie est de trouver la nature de f.

1) Démontrer que f(I)=I
2)a) Démontrez que M' est le barycentre de: (A,2), (B,1) et (M,1).
3)a) Déduisez-en que les points I,M,M' sont alignés.
b) Quelle relation lie les vecteur IM et IM'?
c) Déduisez-en la nature de f

Partie B
C est le cercle d'équation: x²+y²-2x-8y-8=0. Le cercle C coupe l'axe des abscisses en A, d'abscisse négative et en B.
1)a) Construisez C et calculer les abscisses de A et B.
b) Quelle relation lie les vecteurs AO et AB?
2) Un point M décrit C et M' est l'image de M par la transformation f de la partie A
a) Quel est le lieu C' de M'?
b) Construisez C' et trouver une équation de C'

J'ai terminé la Partie A..

OK,

alors maintenant qu'on a la définition de I, je pense que tu as torché (seule ?) la partie A) pour arriver à la conclusion que


Tu as calculé les coordonnées de I ?

Il semble que ton énoncé ne dise pas ce qu'est O.
Si c'est effectivement le centre de ce cercle, il n'y a pas de relation particulière qui lie les vecteurs mentionnés. Ils ne sont pas colinéaires.

Je pense plutôt que O est l'origine du repère. Je vais te dire pourquoi :
Les coordonnées de A et B sont bien celles que tu as trouvées
Alors les coordonnées de I sont (0;0) : c'est l'origine du repère ! Peut-être que ton énoncé a voulu que tu donnes la relation entre et
et alors la relation entre les vecteurs et est


Les propriétés de l'homothétie que tu as dû voir permettent d'affirmer que l'image du cercle de centre (1;4), de rayon 5 par l'homothétie de centre I de coordonnées (0;0), de rapport est un nouveau cercle dont le centre est l'image par cette homothétie du centre du cercle initial et dont le rayon est celui du cercle d'origine multiplié par le rapport d'homothétie.

Mais si tu ne l'as pas vu, il te faut le démontrer dans ce cas particulier.
En passant par les coordonnées, ça ne sera pas trop pénible.

D'ailleurs, ton énoncé te demande une équation de cette image.

Soit M de coordonnées (x;y) appartenant au cercle initial
alors x et y vérifient l'équation x²+y²-2x-8y-8=0
Soit M' de coordonnées (x';y') l'image de M par l'homothétie
alors x' et y' vérifient les équations : à toi de les trouver.

Et dans l'équation du cercle d'origine, substituer x et y par x' et y' pour trouver l'équation de l'image du cercle d'origine par cette homothétie. Ensuite, tu détermineras les caractéristiques de cette image, et tu vérifieras que les propriétés suivent bien les règles que j'ai énoncées dans le cas général.

Au boulot.

Waa, là je suis perdu..
Alors pour répondre à vos questions: La partie A je l'ai faite avec de l'aide, je n'ai pas calculé les coordonnées de I, d'ailleurs je ne sais pas comment les calculer. Dans l'énoncé on ne précise pas ce qu'est O, à mon avis c'est comme vous l'avez dis, le centre du repère?
Et si je dis:
Questions:
1)b) AO = (1/3) AB
2)a) Le lieu de C' est le cercle de centre O (confondu à I) et de rayon 5*1/4 = 5/4
b)Soit M' de coordonnées (x';y') l'image de M par l'homothétie
alors x' et y' vérifient l'équation : (x'-1)² + (y'-4)² = 25/16
=> x'²- 2x' + 1 + y'² - 8y' + 16 - 25/16 = 0
=> x'²- 2x' + y'² - 8y' - 247/16 = 0

Est ce que c'est juste?

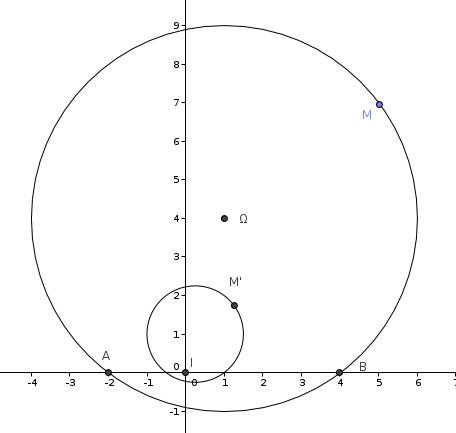
Tu vois bien que sur mon graphique, C' n'a pas pour centre O=I
(rassure-moi : tu arrives au moins à vérifier ça ?)

Trouver les coordonnées de I, tu ne sais pas faire ?

A a pour coordonnées (-2;0)
B a pour coordonnées (4;0)

On cherche les coordonnées de I ? Donnons-leur un nom, temporaire, le temps de les calculer : appelons les



Les coordonnées de sont

Les coordonnées de sont
(tu as repéré les parenthèses dans l'écriture ?

Les coordonnées de sont

Donc nous permet d'écrire deux équations :


Ce qui donne (tu sauras simplifier ?)


C'est quand même le minimum à savoir faire...

Maintenant, les équations de l'homothétie :
Soit M' l'image de M par l'homothétie de centre I, de rapport
Vectoriellement, elle s'écrit donc


On passe aux équations, maintenant qu'on a les coordonnées de I
On appelle (x;y) les coordonnées de M
On appelle (x';y') les coordonnées de M'
On sait que les coordonnées de II sont (0;0)
Alors le vecteur a pour coordonnées
Alors le vecteur a pour coordonnées
Alors le vecteur a pour coordonnées

Et l'équation nous permet d'écrire les équations :


Donc en multipliant les membres des équations par 4, on a aussi


Maintenant, on veut que M soit sur le cercle C, c'est à dire que ses coordonnées vérifient l'équation :


Puisque x=4x' et y=4y', on remplace x par 4x' et y par 4y' (sans oublier les parenthèses)



Ce qui donne


Et en divisant les deux membres par 16


Et en utilisant la forme canonique pour trouver centre et rayon :


En simplifiant, on obtient :




Présenté sous la forme , cela donne


M' est donc sur le cercle de centre , de rayon

J'espère que tout ceci est accessible pour toi, et surtout que tu sauras le refaire si on te le redemande.