Inscription / Connexion Nouveau Sujet
Bonjour,
merci pour ce problème original.
elhor_abdelali a bien avancé dans la résolution du problème mais il n'a pas vu qu'il y avait plusieurs cas à examiner avant de conclure.
J'ai trouvé une CNS très simple sur a,b,c :
 Cliquez pour afficher
Cliquez pour afficherCette fois je suis d'accord.
J'ai une démonstration plus rapide une fois qu'on a trouvé la seule valeur possible pour la constante :
 Cliquez pour afficher
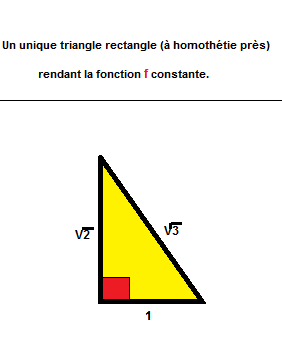
Cliquez pour afficherOn peut remarquer qu'il y a un unique triangle rectangle qui rend
On peut penser à caractériser les triangles du plan rendant la fonction
constante
par leur classe de similitude :
En effet en munissant le plan d'un repère orthonormé direct ,
tout triangle du plan rendant constante est semblable à un unique triangle
où le point décrit la courbe polaire d'équation :
avec .
Bonsoir,
Je propose un peu plus simple avec un arc de cercle :
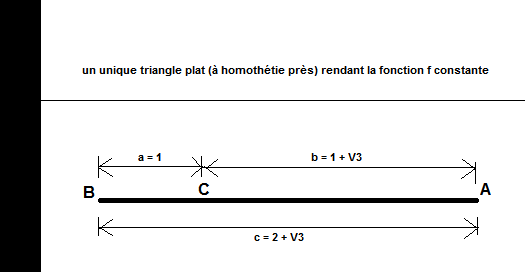
En pointillés, des rectangles particuliers : équilatéral, rectangle et plat.
Si on ne suppose plus a  b
b  c, on peut utiliser le cercle en entier
c, on peut utiliser le cercle en entier 
Bonjour
Petite aparté ...
Le tr rect 1,V3,2 par exemple (et bien d'autres) remplit toutes les conditions non ?
Bonsoir
Je sais bien que les triangles a,aV2,aV3 conviennent. Mais il doit y avoir un trou dans les démonstrations ci-dessus car je trouve plein d'autres triangles qui répondent à la question. As-tu seulement testé le triangle que j'indique ? Je pense que non.
Bonjour,
@derny,
Ton triangle donne f(2) = 2/ 3 , comme tous les triangles.
3 , comme tous les triangles.
Mais f(1) n'est pas égal à 2/ 3 ...
3 ...
Il ne te reste plus qu'à poster le problème suivant :
Caractériser les triangles pour lesquels f(4) = f(2)

je trouve plein d'autres triangles qui répondent à la question



 de voir que
de voir que  sauf erreur de ma part bien entendu
sauf erreur de ma part bien entendu