Inscription / Connexion Nouveau Sujet
Triangle rectangle et produit scalaire
Bonjour à tous,
Voici l'énoncé :
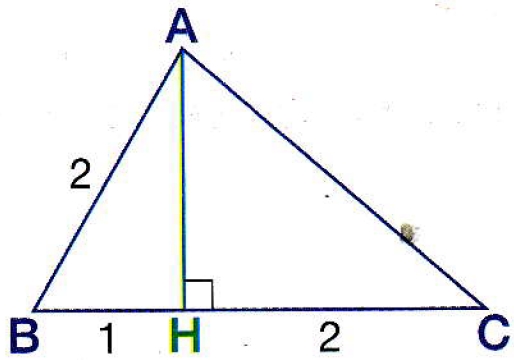
En utilisant les renseignements portés sur la figure, calculez les produits scalaires suivants :
1) ( +
).
2) ( +
).
3) ( +
).(
+
)
Je voudrais juste avoir une confirmation de méthode :
1)On applique le théorème de Pythagore dans le triangle ABH rectangle en H pour trouver la norme de AH. On calcule AB + AH puis on emploie l'expression du produit scalaire utilisant les normes (1/2 de Delta) pour obtenir le scalaire de ce résultat avec AB.
2)On emploie la relation de Chasles pour avoir .
, on calcule AC dans le triangle AHC rectangle en H avec le théorème de Pythagore et on applique AB et AC à la définition déjà utilisée en question 1).
3)On emploie la relation de Chasles pour avoir .
, on trouve un résultat identique à celui de la question précédente (même données, même formule employée).
Je reviens ce soir.
Salut,
oui c'est correct pour le 2) et 3) avec chasles, mais pour conclure tu as besoin des angles entre les vecteur... Je ne comprend pas ce que tu veux dire pour 1). Tu peux aussi simplement utiliser la relation
non idm il n'est peut-être pas besoin des angles des vecteurs .... mais uniquement que de leur cosinus ... comme je vient de le montrer ....
je ne vois pas de différence entre les questions 2/ et 3/ ...
d'ailleurs j'utilise 3/ pour résoudre 2/ ....
Bonjour,
il me semble plus simple de développer les produits.
par exemple pour le 1)
mais ça dépent un peu de ce que vous avez déjà vu en cours.
oui verdurin ... mais on peut le faire sans calculer AH .... même si il y en aura besoin pour la suite ....

Salut cueilleur de jours.
oui verdurin ... mais on peut le faire sans calculer AH .... même si il y en aura besoin pour la suite ....
Je suis d'accord. Et avec le 7 aussi.
Il se trouve que j'ai commencé à taper mon message avant ta réponse, puis j'ai été interrompu, et j'ai continué sans regarder si des réponses étaient arrivées.

Donc j'ai bon pour 2) et 3).
Pour 1), j'utilise la 4ème propriété ici :
http://xmaths.free.fr/1S/cours/cours.php?nomcours=1Spscacours&page=03
Je pensais que ça allait, qu'est ce qui n'est pas correct ?
J'ai effectué, pour la question 1):
* Transformation de (AB + AH).AB en AB.AB + AB.AH
(je n'ai pas mis de flèches mais ce sont bien des vecteurs).
* Calcul de AH = via le théorème de Pythagore.
* Calcul des produits scalaires avec la propriété indiqué dans mon message de 18:46.
* J'obtiens finalement AB.AB + AB.AH = 4 + 2
Il y a un problème, non ?
2/ et 3/ sont égaux par la relation de Chasles
on développe 3/ et on obtient immédiatement le résultat :3 - 2 = 1
...
J'ai dû mal comprendre quelque chose parce que je trouve le même résultat qu'à la 1) aux 2) et 3). Je vous montrerais ce que j'ai écrit cette après-midi vers 16 heures.
Voici ce que j'ai pour l'instant écrit sur ma feuille d'exercice.
(désolé pour la mauvaise qualité de mon écriture).


Alors, ça c'est pour la 3). En fait, il fallait réussir à obtenir des vecteurs colinéaires.
Pour la 2), est-ce correct si on fait :
* (AH + HC).AB = AC.AB
* On calcule AC dans le triangle AHC avec le théorème de Pythagore.
* On remplace dans AC.AB
Comment transformer ceci :
(AH + HC). AB
Avec la relation de Chasles ?
Ou autre chose ? Je suis perdu.
Je ne comprend toujours pas votre message de 19h15.
Si l'on parle de la relation de Chasles, ce serait plutôt : AB = AH + HB (en vecteurs).
2/ et 3/ sont donc bien équivalents puisqu'en utilisant ce théorème dans 2/ on retrouve 3/.
Pour la 3/, il suffit donc juste de marquer "voir 2/".
salut
(AB + AH).AB = AB2 + AB.AH = AB2 + AB.(AB + BH) = 2AB2 - BA.BH = 2AB2 - 2 * 1 * 1/2 = 3
...
D'où vient le 1/2 ?
Le cosinus de ABH ? On n'a pas la mesure de cette angle !
Tu l'as calculé avec cos = adjacent / hypoténuse, c'est ça ?



