En troisième tu sais ce que sont les triangles isométriques ?

Ouii ouii ^^

Rappel : une hauteur est un segment issu d'un sommet et perpendiculaire au côté opposé à ce sommet.

Mais même, quel est le rapport entre isométrie est le fait d'être isocèle, car pour parler d'isométrie il fuat au minimum deux triangles?

En coupant le triangle en 2 grâce à l' hauteur
T' as 2 triangles

Là je suis d'accord !

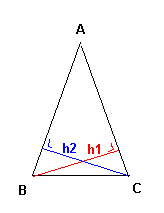
Soit h1 et h2 les 2 hauteurs de même longueur

Aire(ABC) = (1/2)*AB*h2
Aire(ABC) = (1/2)*AC*h1

--> (1/2)*AB*h2 = (1/2)*AC*h1

AB*(h2/h1) = AC
et comme h1 = h2, on a h2/h1 = 1 -->

AB = AC
Le triangle a 2 cotés de même longueur, il est donc isocèle.
-----
Sauf distraction.  

Essaie avant tout de faire la figure et de mettre les données que tu peux.

Mercii
C' est pas comme sa qu' on fait non plus lol
Mais merci

Fais donc ce qu'a expliqué J-P ! Et  il n'y a même pas besoin de parler d'isométrie, vois-tu ?

Ah pas mauvaise idée avec l'aire J-P sauf que ça ne fait pas appel à l'isométrie

Moi, en appelant M le pied de la hauteur issue de C et N le pied de la hauteur issue de B, j'aurais montré que AMC et ANB étaient isométriques, donc AM=AN, puis que BMC et BNC sont aussi isométriques, d'où BM=CN.

Bonjour,

Je suis d'accord, mais comment montrer que MCB a même mesure que NBC pour conclure ?

bonsoir
les angles ABN et ACM sont égaux car ils ont un angle complémentaire commun : BAC
donc ils ont le même cosinus et BN/AB = CM/AC

Bonsoir à vous deux Benta25 et plumemeteore

Cette question aura 1 an dans quelques jours ! En espérant que Lachtitemiss n'ait plus besoin de la réponse !