Inscription / Connexion Nouveau Sujet
triangles semblables
Bonjour,
je bloque sur un exercice :
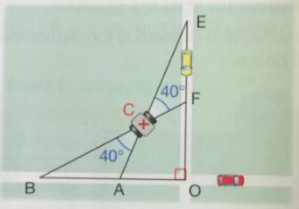
une double caméra (C) permet de surveiller deux rues perpendiculaires [OE] et [OB] selon deux angles de 40°. quelle doit être la valeur de la mesure de l'angle pour que les triangles ABC et CEF soient semblables ? (cf photo)
J'ai noté x l'angle pour poser une équation, j'obtiens donc
= 140-x mais je ne parviens pas à finir cette exercice ...
Merci d'avance pour vos réponses
Bonjour
écris ainsi (en fonction de ce x) de proche en proche tous les angles de la figure ...
enfin pas tous tous, certains autres suffisent... mais dans le doute et si tu ne vois pas lesquels, tous.
écris ensuite que les triangles doivent être semblables
ça donne une équation en x.
ce n'est pas dans cet ordre là que je te proposais les calculs !
mais qu'importe.
surtout tu dois obligatoirement justifier chaque angle que tu calcule.
(sinon aucun espoir de prouver quoi que ce soit, ce ne serait que des affirmations sans aucune preuve et qui ne risquent donc pas d'aboutir à quoi que ce soit)
et puis il y en a d'autres des angles !!! vu que tu n'as en fait pas choisi les bons, continue et calcules les tous, absolument tous.
tu rédigeras avec les seuls intéressants ensuite)
FCB est un angle plat donc FCA + ACB = 180 donc FCA = 180 - 40 = 140°
ECA est un angle plat donc ECB + ECF = 180 donc ECB = 180 - 40 = 140°
BAO est un angle plat donc BAC + CAO = 180 donc CAO = 180 - (140 - x) = 40 + x
c'était valable surtout pour les premiers que tu avais cité :
j'ai donc ABC = x OK c'est le point de départ, on pose ABC = x
BAC = 140-x logiquement c'est ensuite : parce que la somme des angles de ABC = 180° et que la ligne d'après. :
BCA = 40 dans l'énoncé (et donc BAC)
CEF = 140-x faux
CFE = x pourquoi ??
FCE = 40 dans l'énoncé (mais de toute façon, angle opposé par le sommet à BCA)
FCB est un angle plat donc FCA + ACB = 180 donc FCA = 180 - 40 = 140° OK (mais ne servira à rien)
ECA est un angle plat donc ECB + ECF = 180 donc ECB = 180 - 40 = 140° idem
BAO est un angle plat donc BAC + CAO = 180 donc CAO = 180 - (140 - x) = 40 + x OK
il y a d'autre angles ...
déja corriger et compléter la raison que tu as choisie pour affirmer ça :
CEF = 140-x pourquoi ?? faux
CFE = x pourquoi ?? faux
c'est toi qui prétends qu'ils ont ces valeurs là !
(sans justification ni preuve)
les angles qui servent vraiment sont en rouge dans cette figure
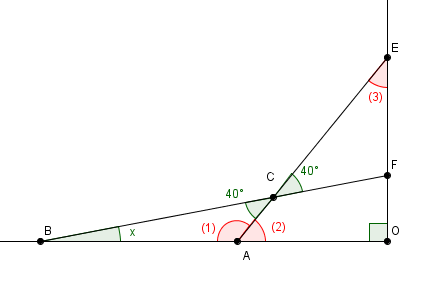
avec ma méthode que je te proposais qui évite de se planter sur lesquels angles sont égaux ou pas.
dans un premier temps ignorer complètement si les triangles sont semblables ou pas
et calculer (vraiment) les angles en rouge en fonction de x, dans l'ordre des numéros
et ensuite seulement on se préoccupera de la similitude des triangles
d'accord merci !
je me suis effectivement emmêler les pinceaux avec CEF et CFE
je trouve donc :
(1) BAC = 180 - 40 - x = 140 - x
(2) CAO = 180 - (140 - x) = 40 + x
(3) AEO = 180 - (40 + x) - 90 = 50 - x
Est-ce exact ?
OK
et maintenant pour que les triangles soient semblables il faut (on sait déja les angles de 40°)
soit que CEF = ABC
soit que CEF = BAC
ça donne des équations en x dont une seule aboutit à quelque chose
(l'autre étant clairement impossible, c'était en plus celle que tu avais choisie, celle qui est impossible !)
avec l'adresse de ton prof, on pourrait même lui envoyer directement la correction, qu'en penses-tu ?

(modérateur)
en lisant la discussion et en continuant les calculs ...
on en était là (relire).
soit que CEF = ABC (alias AEO = x) et AEO est dans le message au dessus)
équation en x à (tenter de) résoudre
et
soit que CEF = BAC (alias AEO = BAC, AEO et BAC au même endroit dans la discussion)
autre équation en x à (tenter de) résoudre
une seule des deux aboutira, mais tant qu'on ne les a pas écrites (c'est du copier-coller ! faut pas pousser !) et tenté de les résoudre on ne sait pas laquelle des deux.


