Inscription / Connexion Nouveau Sujet
Triangles semblables
Bonsoir,
Je voudrais des indices pour l'exo suivant :
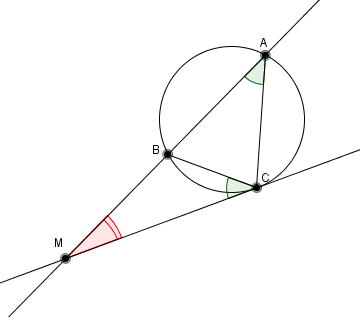
Soit ABC un triangle et (C) son cercle circonscrit .
La tangente au cercle (C) au point C , coupe (AB) en M.
Démontrer : (AC×AC/BC×BC)=MA/MB .
Bonjour,
avec un titre "triangles semblables" peut être faudrait-il chercher des triangles semblables dans la figure,
avec des angles
des angles inscrits par exemple
rappel : le cas limite d'un angle inscrit quand l'un des côtés est une tangente ...
Bonjour,
L'angle ^c est isometrique à l'angle ^A
Sont deux angles inscrits limitants l'arc BC ne contenant pas A.
Donc MC/MA =BC/AC=BC/MB.
Aprés je suis bloqué.
Merci de me faire avance
Pas d'accord
L'angle ^c est isometrique à l'angle ^A
reste à dire tout de même de quels angles tu parles !!!
si c'est les angles du triangle ABC (seuls angles qui supportent de ne pas écrire leur nom complet à trois points) c'est totalement faux.
on va dire que tu parlais bien des angles BCM et BAC
donc ... ta relation est fausse, d'ailleurs sa partie BC/AC=BC/MB. voudrait dire que AC = MB !!!
alors que selon la forme du triangle M peut être aussi on que l'on veut (si le triangle est presque isocèle en C)
les triangles semblables sont MAC et MCB (dans cet ordre) :
MC/MA = MB/MC = CB/AC
deux lettres du haut en correspondance avec deux lettres du bas quand on écrit les sommets correspondants les uns au dessous des autres :
MCB
MAC
ce qui s'écrit
AC/BC = MA/MC
et AC/BC = MC/MB
... et on cherche à calculer (AC/BC)*(AC/BC) en fait, non ?


