Inscription / Connexion Nouveau Sujet
Triangles semblables à côtés parallèles
Bonjour,
Mon professeur m'a demandé de prouver que deux triangles ABC et A'B'C' ayant leurs côtés parallèles sont semblables. Je ne sais pas du tout comment m'y prendre. La seule contrainte que j'ai, c'est de pas utiliser le cas de similitude A-A des triangles semblables car c'est grâce aux triangles à côtés parallèles qu'il vaut le prouver ce cas.
Merci d'avance.
Bonjour,
une possibilité inspirée par le titre.
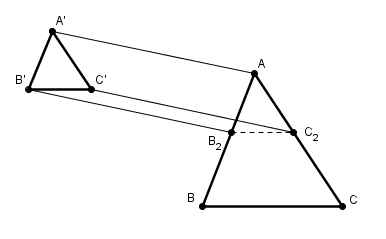
hypothèse ABC et A'B'C' parallèles
construction :
tracer AA'
la parallèle à AA' passant par B' coupe (AB) en B2
la parallèle à AA' passant par C' coupe (AC) en C2
prouver (en considérant les parallélogrammes) que B2C2 est alors parallèle à BC
on peut alors appliquer Thalès à ABC / AB2C2
Un tout grand merci mais je suis vraiment nul. Je ne comprends pas pourquoi en appliquant thales cela prouve que les deux triangles sont semblables
la construction consiste à construire un triangle AB2C2 isométrique (les parallélogrammes) à A'B'C'
et à justifier pourquoi cette construction conduit à B2C2 parallèle à BC
AB2C2 est alors d'après Thalès tel que AB2/AB = AC2/AC = B2C2/BC
et comme on a prouvé que AB2 = A'B', AC2 = A'C' et B2C2 = B'C' c'est fini :
A'B'/AB = A'C'/AC = B'C'/BC et les triangles ABC et A'B'C' sont donc semblables.
en fait tout est dans la rédaction correcte de tout ça, en évitant de prendre ses désirs pour des réalités
(que B2C2 serait directement parallèle et égal à B'C', il faut le prouver)
Et si à la place de construire ces parallélogrammes, je construisais une parallèle à [B'C'] directement et que je notais les intersections entre cette parallèle et les côtés du triangles C2 et B2. Cela ne serait pas correct?
le problème est que cette parallèle de donnerait pas directement une relation entre les triangle AB2C2 et A'B'C'
donc certes AB2C2 serait semblable à ABC
mais on ne pourrait pas en tirer directement quoi que ce soit pour A'B'C'


