Inscription / Connexion Nouveau Sujet
Trigonométrie
Bonjour , j'aimerais avoir de l'aide pour cet exercice s'il vous plait :
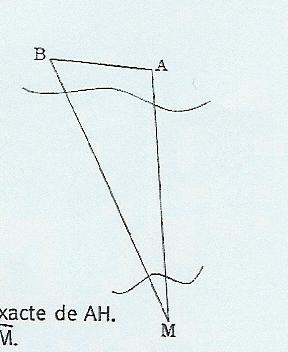
Deux points A Et M sont situés de part et d'autre d'un bras de mer.
AB = 6,2 km.
= 100°
= 60°
On appelle H le pied de la hauteur issue de A du triangle ABM.
1. Calculer la valeur exact de AH :
Ma réponse :
Nous savons qu'une hauteur est une droite qui passe par un sommet et qui coupe le côté opposé perpendiculairement.
Puisque (AH) , issue de A, est une hauteur , alors , (AH)(BM).
Nous savons qu'un triangle rectangle est un triangle qui a un angle droit de 90°.
Puisque (AH) (BM) , alors , AHB est un triangle rectangle.
Dans le triangle AHB , rectangle en H , je peux utiliser la Trigonométrie :
cos =
cos 60° =
AH = cos 60°6,2
AH = 3,1 km.
2. Calculer l'angle .
3. Calculer la valeur exacte de AM puis une valeur décimale approchée à 0,1 km près.
Je n'ai pas trouvé pour le moment les deux dernières.
Merci d'avance de votre aide.i
Fly22
Bonjour
cos B = ... est faux
Dans le triangle ABH, rectangle en H, tu connais
l'angle B
l'hypoténuse AB
et tu cherches le côté opposé AH
Il faut donc utiliser ...
Ahhhhhh oui , en fait j'ai fais un figure à main levée où la hauteur paraissait être l'hypoténuse. Merci de me l'avoir indiqué.
Pour la question 2. , j'ai trouvé que la mesure de = 30°.
Donc après tout ces calculs , j'ai trouvé :
1. Nous savons qu'une hauteur est une droite qui passe par un sommet et qui coupe le côté opposé perpendiculairement.
Puisque (AH) , issue de A, est une hauteur , alors , (AH)(BM).
Nous savons qu'un triangle rectangle est un triangle qui a un angle droit de 90°.
Puisque (AH)[tex\perp][/tex] (BM) , alors , AHB est un triangle rectangle en H , ainsi que le triangle AMH.
Dans le triangle AHB , rectangle en H , je peux utiliser la Trigonométrie :
sin =
sin 60° =
AH = sin 60° 6,2 ( Valeur exacte ).
2. Dans le triangle AHB , rectangle en H , je peux utiliser la Trigonométrie :
cos =
cos =
= 30°
Puisque = 100°
Alors , =
-
= 100° - 30°
= 70°
3. Dans le triangle AMH, rectangle en H, je peux utiliser la Trigonométrie :
cos =
cos 70° =
AM = ( Valeur Exacte )
AM 15,7 km. ( Valeur approchée à 0,1 km près ).
Bon Et Bien voilà , j'espère que c'est bon.


