Inscription / Connexion Nouveau Sujet
Trigonométrie
Bonjour tout le monde, et merci de m'accorder un peu de votre temps.... 
Il y a dans mon livre de math (phare 3eme nouvelle édition, exo 44p229) un exercice sur la trigonométrie que je n'arrive pas a faire. Je ne demande pas de réponses, juste une petite astuce, un petit indice qui pourrait me mettre sur la voie de celle-ci.^^
(réaliser un schéma pour que ce soit plus clair)
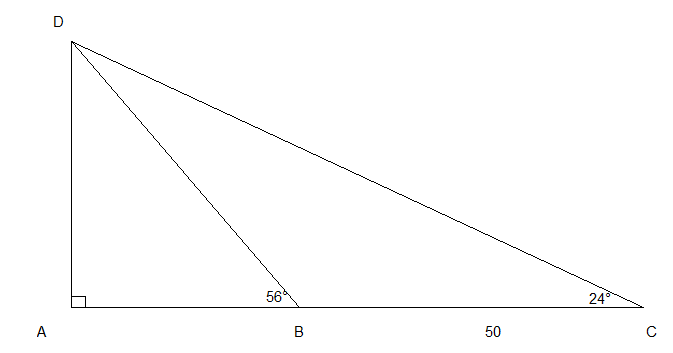
-Les points A, B et C sont alignes, CB=50m
-Les triangle ABD et ACD sont rectangles en A.
-l'angle ABD=56 degrés l'angle ACD= 24 degrés
Et on nous demande de calculer l'arrondi au mètre prés de la longueur AD.
Cependant on n'a que des mesures d'angles alors je ne sais pas trop comment utiliser la trigonométrie dans cet exercice. (cela m'embête beaucoup car d'habitude je suis plutôt forte en math...)
J'apprécierais beaucoup votre aide, merci d'avance 
bonjour
Ma démarche est la suivante : nous avons plein d'inconnues : AB, AD, CD et BD
4 inconnues : il faut donc trouver 4 équations
Voilà les 4 équations :
cos(24)= (AB+50)/CD
cos(56) = AB / BD
BD² = AD² + AB²
CD² = AD² + (AB+50)²
donc on peut résoudre ce système de 4 inconnues à 4 équations ... maintenant reste à le faire :
- il faut développer l'expression (AB+50)²
- puis trouver des substitutions astucieuses pour trouver AD

Oui, mais les équations ne peuvent pas être calculées parce que il y a trop d'inconnue. 
Comment faire alors?
cos(24) = (AB+50)/CD
cos(56) = AB / BD
BD² = AD² + AB²
CD² = AD² + (AB+50)²
a = cos(24°) = 0,91354545764260089550212757198532
b = cos(56°) = 0,55919290347074683016042813998599
c = sin(56°) = 0,82903757255504169200633684150164
et en sachant que b² + c² = 1
Appelons d = b/c (cela simplifiera l'écriture à la fin).
De toutes façons, a, b, c et donc sont des constantes et on ne s'en occupera qu'à la fin de la résolution
Nommons les inconnues : il y en a 4 :
x = AB
y = CD
z = AD ==> c'est elle que l'on cherche
t = BD
Le système d'équations s'écrit alors :
a = (x+50)/y
b = x / t
t² = z² + x²
y² = z² + x² + 100x + 2500
On enlève déjà une inconnue : le « t »
De l'équation n°2 on t = x/b qu'on remplace dans l'équation n°3.
Il reste 3 équations et 3 inconnues ; on progresse:
a = (x+50)/y
x² = b²z² + b²x²
y² = z² + x² + 100x + 2500
De la 1ère équation on sort y= que l'on remplace dans la troisième équation
y = x/a + 50/a
Il reste 2 équations à deux inconnues (on n'a jamais été aussi près du but !)
x² = b²z² + b²x²
x²/a² = z² + x² + 100x + 2500
soit en simplifiant :
b²z² = (1-b²)x² soit b²z² = c²x² soit encore bz = cx
z² = x²/a² - x² - 100x - 2500
De la première équation on a x que l'on remplace dans la deuxième équation
x = bz / c
z² = (b²z² / c²) / a² - b²z² / c² - 100bz/c - 2500
z² = b²/c²a² z² - b²/c² z² - 100bz/c - 2500
z² (1 + b²/c² - b²/c²a² ) + 100b/c z - 2500 = 0
(1 + d² - d²/a²) z² + 100d z - 2500 = 0
Et nous voilà arrivés à une super équation à une inconnue mais mais mais mais mais du deuxième degré (z²)
Il existe une méthode pour la résoudre mais je doute que ce soit du programme de troisième.
Est-ce bien un exercice de niveau 3ème ?
… ou est-ce que je ne suis pas parti un petit peu trop loin et n'ai pas vu une méthode plus simple ?
Est-ce que quelqu'un peut nous donner son avis sur ce gros foutoir ? Je suis à la recherche d'une solution plus simple mais je ne vois toujours pas d'astuce ! ! !
Est-ce que l'énoncé est complet ?
Oui, l'énoncé est complet.
Mais je pense que vous êtes aller chercher loin parce que je n'ais pas compris. Mais vous avez la bonne figure sauf que (AB), et plus grand que (AC)
Bonjour,
Dans chacun des triangles ABD et ACD :
AD = AB * tan 56
AD = (AB+50) tan 24
=> AB* tan 56 = (AB + 50) * tan 24
AB* tan 56 = AB *tan 24 + 50 *tan 24
AB tan 56 - AB tan 24 = 50*tan24
AB (tan 56-tan24) = 50*tan24
AB = (50*tan24)/(tan 56-tan24)
La valeur trouvée pour AB => AD = AB*tan56
Coucou me revoilou
En y réfléchissant au calme et sur papier j'ai trouvé la solution
Dans le triangle ABD on a
cos(56°) = AB/BD
sin(56°) = AD/BD
on les divise pour faire disparaître BD ce qui donne : Cos(56) / sin(56) = AB/AD
Dans le triangle ABD on a
cos(24°) = AC/CD
sin(24°) = AD/CD
on les divise pour faire disparaître CD ce qui donne : Cos(24) / sin(24) = AC/AD
Pour simplifier appelons AB = d et la valeur cherchée AD = x
on : Cos(56) / sin(56) = d/x
et Cos(24) / sin(24) = (d+50)/x
2 équations simples à 2 inconnues : ca se résoud the fingers in the nose pour arriver au résultat final :
x = 50 / ( cos24/sin24 - cos56/sin56 )
Yapluka prendre la calculette pour trouver les cos et les sin et le tour est joué.
Ouf ! ! ! 

 J'ai réussie, merci infiniment!
J'ai réussie, merci infiniment!



