Inscription / Connexion Nouveau Sujet
Un bel hexagone bleu
Bonjour,
Bonjour à tous ,
Un peu de géométrie (facile)
Je viens de travailler sur les angles dans le triangle équilatéral,
en cherchant des angles de 
/12 j'ai trouvé une belle figure bleue.
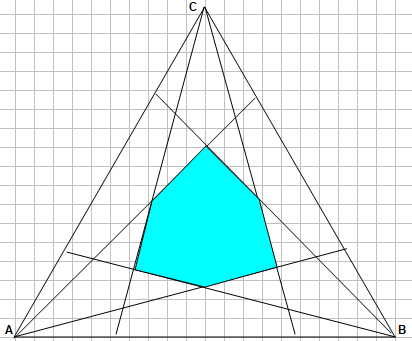
Quelle est l'aire de ce polygone si AB =1 ?
Bonjour Dpi
On note I le pied de la hauteur issue de C , O le centre du triangle et J le point de [CI] tel que IJ=IA .
Cliquez pour afficherImod
* Modération > Messge édité à la demande de l'auteur : 3G remplacé par 2G*
C'est normal , il manquait un morceau dans ma différence 
J'ai trouvé un nouveau découpage de la zone bleue qui a l'air prometteur , il faut que j'approfondisse un peu .
Imod
Mon idée en partant de la zone en bleu .
Cliquez pour afficher
A partir de là , il est facile de construire le triangle bleu et de calculer son aire .
Imod
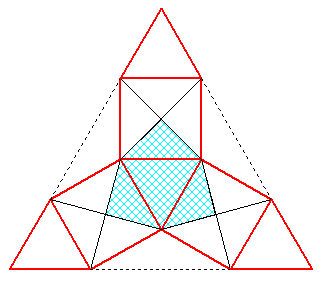
En effet , il suffit de compter le nombre de triangles équilatéraux et de carrés dans la figure complète et dans la partie bleue .
Imod
J'aime bien cette figure
>Imod
J'aime bien ton approche du 3 à 10h56 ,il ne manque que le résultat..
>Sylvieg
Ce n'est pas exact mais c'est l'ordre d'idée
>derny
Tu dois avoir une erreur car ta réponse est supérieure à la surface du triangle de coté1
Bonjour,
Je n'ai pas les mêmes résultats
Les angles de l'hexagone sont de 90° et 150° (3 de chaque sorte).
Les 6 cotés ont la même mesure, soit :
L'aire est
Les 6 cotés ont la même mesure, soit :
Mais je ne suis pas passée par là.
J'ai utilisé la longueur des segments rouges de la figure de Imod :
>Sylvieg
Mes plus plates excuses j'avais mal vérifié ta formule qui d"ailleurs est la plus simple .
>derny ok
à tous
Excuses acceptées dpi
J'ai bien aimé refaire plusieurs fois mes calculs pour ce bel hexagone.
La figure d'Imod m'a bien aidée.
Bonjour. Tout le monde est maintenant d'accord avec 2.25 - 1.25V3. Le résultat est "simple" mais demande quand même quelques calculs avant de l'obtenir.
Annuler
connectez vous