Inscription / Connexion Nouveau Sujet
Un prisme dans un cylindre
Bonjour, j'ai un DM à rendre pour demain et je ne comprend pas l'exercice, pouvait l'aidé s'il vous plait merci
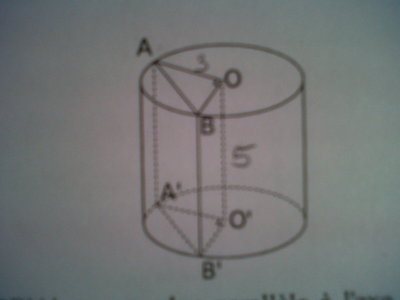
Un cylindre à pour hauteur [OO'] mesurant 3 cm et pour rayon [OA] mesurant 3 cm. On coupe ce cylindre par 3 plans parallèles à l'axe d'un cylindre de sorte que le triangle AOB soit rectangle en O. Les 3 actions obtenues ABB'A', OBB'O' et AOO'A' sont des rectangles.
a) Quelle est la nature exacte du triangle AOB ? Justifie
b) Calcule la valeur exacte de AB.
c) Calcule l'aire du rectangle ABB'A' arrondie au dixième.
d) Calcule le volume du cylindre. Arrondis au 10e de cm3.
e) Calcule le volume du prisme droit AOBA'O'B'.
f) Quel pourcentage du cylindre me prisme droit AOBA'O'B' représente-t'il ? Arrondie à l'unité.
g) Calcule l'aire latérale du solide AOBA'O'B. (C'est la somme des aires des 5 faces de ce solide)
Désolé je n'arrive pas à mettre la figure mais j'ai trouvé la même, cliqué sur le lien https://www.ilemaths.net/sujet-triangle-rectangle-dans-un-cylindre-3eme-558018.html C'est le même sans le 5 qui est écrit sur la figure
a) Quelle est la nature exacte du triangle AOB ? Justifie
e de sorte que le triangle AOB soit rectangle en O
que peux-tu dire des côtés OA et OB?
rectangle, ça on le sait car c'est directement écrit dans l'énoncé
on t'en demande plus
question réitérée :
que peux tu dire de OA et OB ?
(pas à l'oeil sur la figure, en imaginant un vrai cercle en vrai)
d'ailleurs toutes ces réponses et même les errements avant d'y arriver sont dans la discussion que tu as citée !!
kenavo27 : OK, je continue à suivre la discussion et interviendrais au besoin.
tu as vraiment déje vu des parallèles qui ont le point O en commun ??
(réponse déja signalée comme fausse par kenavo27, tu les lis ?)
on te parle de cercle, peux tu dire ce que sont OA et OB pour ce cercle ?
non.
d'abord tu ne répond pas à la question que je t'ai posée mais à une autre
et ensuite le "centre" de deux points ça ne veut rien dire de toute façon
on pourrait parler du milieu de deux points (raccourci pour dire le milieu du segment défini par ces deux points), mais alors A, O et B seraient alignés !!
(l'angle AOB est loin de valoir 180°, il vaut 90°, dit l'énoncé)
ma question porte sur les segments [OA] et [OB] dans un cercle de centre O, et A et B sur ce cercle
que sont ces segments ?
et que peut on dire de leur mesure OA et OB ?
(j'ai l'impression que tu ne sais pas lire correctement
et donc que tu n'arrives même pas à lire la réponse correcte écrite dans la discussion que tu as citée !!)