Inscription / Connexion Nouveau Sujet
un problème ...de bijouterie
Re
Je ne me présente plus sur le forum... lol
Bon c'est super sympa de votre part si vous me corriger mes erreurs de cet exercice :
Une bijouterie confie à un artisan joaillier le travail suivant: il doit réaliser des bracelets de deux types , A et B.
Chaque bracelet de type A demande 2 h de travail et nécessite 10g d'or.
Chaque bracelet de type B demande 3 h de travail et nécessite 25g d'or.
Le délai imposé à l'artisan fait qu'il ne peut disposer, au maximum, que de 42 heures de travail.
Le bijoutier exige au moins 5 bracelet de chaque type, et fournit 250g d'or au joaillier pour ce travail. Soit X le nombre de bracelet de type A et y le nombre de bracelets de type B.
Déterminer graphiquement tous les couples ( x, y) possibles compte-tenu des contraintes imposées à l'artisan.
Donc=
x+y = xy
(x) x 5=y
y x 5 = x
Pour 5 bracelets =
Type A =
5 x 10 = 50 g
5x2 = 10h
Type B =
5x25=125g
5x3 = 15h
Donc
125+50 = 175 g
250-175 = 75g
10+15 = 25h
42-25=21h
Sa fait qu'en 25 h il fait 10 bracelets, 5 de type A et 5 de type B avec 175g d'or, il lui reste 21h et 75g d'or.
X=5 et y = 5
Sinon type A= 10x10 = 100g
10x2 = 20h
Type B= 6x25= 150g
6x3 = 18h
Donc
100+150 = 250 g
18h+30h = 38 h
42-38= 4h
Le joaillier aura utiliser les 250 G d'or et il lui restera 4h et aura fait 10 bracelets de type A et 6 bracelets de type B.
X=10 et y =6
Ou Type b = 10x25 = 250g
10x3= 30h
42-30= 12H
Le joaillier aura utiliser les 250 G d'or et il lui restera 12 h et aura fait 10 bracelets de type B
Y = 10
Pour le graphique , les couples (x;y) sont : (5;5) , (10;6) et (10;0)
J'espère avoir compris l'exercice, pour la question il y a certainement d'autres combinaisons possibles avec type A + type B, mais bon deux ou trois exemples suffiront !
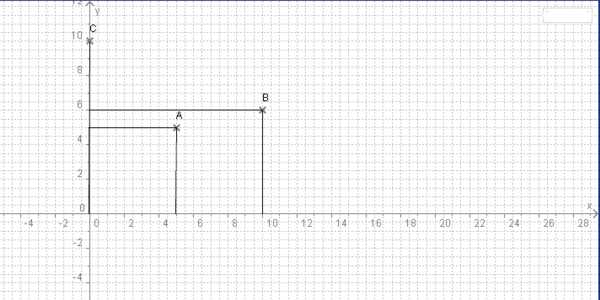
Je pense que tu dois voir le probleme un peu différent
et décrire une zone répondant à la problèmatique:
bracelet A = X
bracelet B = Y
1ère droite:
10x+25y=250
2ème droite:
2x+3y=42
3ème droite
x+y=10
et l'intersection des 3 droites donnent une zone correspondant au probleme
Comprends tu mes explications?
Les contraintes résultant de l'énoncé sont:
x et y entiers
x >= 5
y >= 5
2x + 3y <= 42
10x + 25y <= 250
---
Soit:
x et y entiers
x >= 5
y >= 5
y <= 14 - (2/3)x
y <= 10 - 0,4x
---
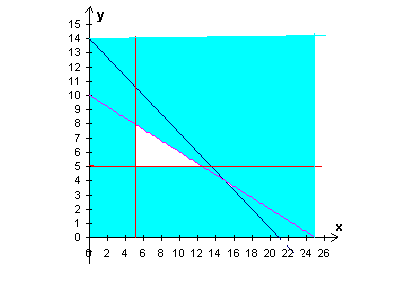
On reporte ces contraintes sur un graphique (les zones bleues sont interdites).
Il reste donc la zone triangulaire blanche (avec ses bordures) comme permise, mais seuls les points coordonnées entières conviennent:
Soit les couples (x,t) tels :
(5,5) ; (6,5) ; (7,5) ; (8,5) ; (9,5) ; (10,5) ; (11,5) , (12,5)
(5,6) ; (7,6) ; (8,6) ; (9,6) ; (10,6)
(5,7) ; (6,7) ; (7,7)
(5,8)
Tous ces couples conviennent car ils respectent les contraintes.
---
Bien que ce ne soit pas demandé dans l'énoncé, on peut sélectionner les couples qui utilisent le plus d'or possible.
Il reste alors les couples (12,5) ; (10,6) ; (7,7) et (5,8)
---
On vérifie:
Le couple (12,5)
Il demande 12*2 + 5*3 = 39 heures de travail et utilise 12*10 + 5*25 = 245 g d'or.
Le couple (10,6)
Il demande 10*2 + 6*3 = 38 heures de travail et utilise 10*10 + 6*25 = 250 g d'or.
Le couple (7,7)
Il demande 7*2 + 7*3 = 35 heures de travail et utilise 7*10 + 7*25 = 245 g d'or.
Le couple (5,8)
Il demande 5*2 + 8*3 = 34 heures de travail et utilise 5*10 + 8*25 = 250 g d'or.
-----
Sauf distraction.