Inscription / Connexion Nouveau Sujet
!! Vecteur/scalaire?somme minimale? formule de la médiane
* Modération > *** Bonjour *** *
Soient deux points A et B distincts, et d une droite différente de (AB).
Comment choisir un point M sur la droite d de telle façon que la somme MA2 + MB2 soit la plus petite possible ?
On peut penser à utiliser le théorème de la médiane après avoir introduit le point I, milieu du segment [AB].
Après avoir obtenu MA2+ MB2= 2MI2+ IA2 + IB2, on remarquera que le deuxième membre est minimal lorsque la longueur MI est minimale, ce qui est réalisé par un unique point qu'il faudra définir.
Bonjour,
Je vois que tu es nouveau, bienvenue sur l'
Ton premier message manque singulièrement de convivialité...
A LIRE AVANT DE POSTER OU DE RÉPONDRE, MERCI (Clique sur ce lien).
Prends le temps de lire ce sujet, en particulier le point 3., et complète ta demande en restant dans le même sujet.
Quelqu'un va te venir en aide.
Merci pour votre réponse mais je ne voit pas trop j'ai essayé de faire la formule de la médiane pour relier M à I en faisant MA+AI
Pouves vous me dire pourquoi il faut placer un point H et faire la relation de Charles plutôt que les points À et B
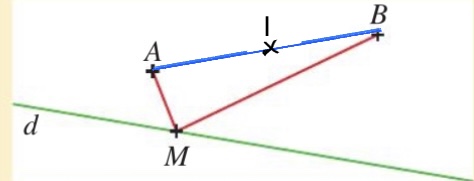
tu n'as pas tracé la droite (AB) mais le segment [AB] !!
mais bon gardons la droite d et le point M sur d et le point I.
où faudrait-il placer M pour que la distance MI soit minimale ?
J'ai essayé avec géo gebra : il faut déplacer le point M de façon à ce qu'il soit avec MI parallèle à AB
Annuler
connectez vous