Fiche de mathématiques
Ile mathématiques > maths 1ère > Trigonométrie et fonctions trigonométriques
1. Peux-tu en déduire cos x ?
2. On sait de plus que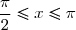
.
Trouver cos x et tan x.
)
.
2. Calculer)
.
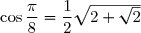, calculer le cosinus de 
.
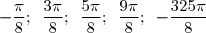Ainsi, cos² x = 1 - sin² x.
Donc :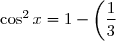^2 = \dfrac{8}{9} \text{ soit } \cos x = \dfrac{2\sqrt{2}}{3} \text{ ou } \cos x = -\dfrac{2\sqrt{2}}{3})
.
On ne peut pas en savoir plus.
2. Sachant que![x \in \left[\dfrac{\pi}{2}; \pi\right]](https://latex.ilemaths.net/latex-0.tex?x \in \left[\dfrac{\pi}{2}; \pi\right])
, alors 
.
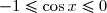Donc d'après ce qui précède on peut écrire :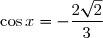
Puis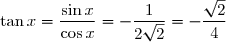
.
On commence par déterminer la mesure principale de l'angle, c'est-à-dire la mesure comprise dans![]-\pi\;;\pi]](https://latex.ilemaths.net/latex-0.tex?]-\pi\;;\pi])
1.
.
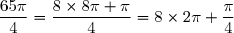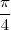est la mesure principale de l'angle 
.
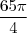Comme pour tout entier relatif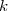
; =\cos (x) )
On obtient :=\cos\left(\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2})
2. Procédons de même.
.
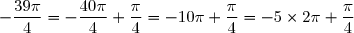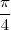est la mesure principale de l'angle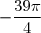 
Par conséquent :=\sin \left(\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2})
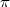/2)= -sin(x) ; cos(x+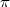) = -cos(x) ; cos(x+2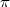) = cos(x) ; cos(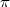-x) =-cos(x) ; cos(/2-x) = sin(x).
Calculons)
: =\dfrac{2-\sqrt{2}}{4})
et >0 donc: =\dfrac{1}{2} \sqrt{2-\sqrt{2}})
=\cos\left(\dfrac{\pi}{8}\right)=\dfrac{1}{2} \sqrt{2+\sqrt{2}})
=\cos\left(\dfrac{4\pi-\pi}{8}\right)=\cos\left(\dfrac{\pi}{2}-\dfrac{\pi}{8}\right)=\sin\left(\dfrac{\pi}{8}\right)=\dfrac{1}{2} \sqrt{2-\sqrt{2}})
=\cos\left(\dfrac{\pi}{2}+\dfrac{\pi}{8}\right)=-\sin\left(\dfrac{\pi}{8}\right)=-\dfrac{1}{2} \sqrt{2-\sqrt{2}})
=\cos\left(\pi+\dfrac{\pi}{8}\right)=-\cos\left(\dfrac{\pi}{8}\right)=-\dfrac{1}{2} \sqrt{2+\sqrt{2}})
=\cos\left(\dfrac{325\pi}{8}\right))
et =\cos\left(20\times \left(2\pi\right)+\dfrac{5\pi}{8}\right)=\cos\left(\dfrac{5\pi}{8}\right)=-\dfrac{1}{2} \sqrt{2-\sqrt{2}})
.Publié par Tom_Pascal
le
Trigonométrie
exercice 1
x est un réel tel que sin x =1. Peux-tu en déduire cos x ?
2. On sait de plus que
Trouver cos x et tan x.
exercice 2
1. Calculer2. Calculer
exercice 3
Sachant queexercice 1
1. On sait que cos² x + sin² x = 1 pour tout réel x.Ainsi, cos² x = 1 - sin² x.
Donc :
On ne peut pas en savoir plus.
2. Sachant que
Donc d'après ce qui précède on peut écrire :
Puis
exercice 2
On commence par déterminer la mesure principale de l'angle, c'est-à-dire la mesure comprise dans
1.
Comme pour tout entier relatif
On obtient :
2. Procédons de même.
Par conséquent :
exercice 3
cos(-x)=cos(x) ; cos(x+Calculons
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Voir la correction