Fiche de mathématiques
Ile mathématiques > maths 3ème > Développement et factorisation
Fiche relue en 2016.
Remarques :
1. La lecture de ces résultats de gauche à droite comme écrit ci-dessus permettent de développer des produits.
Une lecture de droite à gauche permettrait de factoriser des expressions. Effectivement, on obtient alors :
a² + 2ab + b²=(a + b)²
a² - 2ab + b²=(a - b)²
a² - b²=(a - b)(a + b)
2. Devant une différence de deux termes qu'on a à factoriser, il sera bon de penser à l'identité remarquable
a²-b²=(a-b)(a+b)
Exemple : factoriser x²-7 ; repérer que 7 est le carré de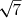 et alors, on pourra écrire
et alors, on pourra écrire
(x+\sqrt{7}))
3. Il est d'usage de présenter les résultats des développements sous forme ordonnée suivant les puissances d'une variable choisie.
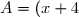^2\\ B = (5 + x)^2\\ C = ( 3 x + 7)^2\\ D = (2 x + 3)^2\\ E = (7 + 2 x)^2\\ F = (3 + 4 y)^2\\ G = (x - 2)^2\\ H = (2 x - 5)^2\\ I = (3 - 2 x)^2\\ J = (7 x - 3)^2)
(x + 7)\\ L = (2 x - 3)(2 x + 3)\\ M = (3 x + 7)(3 x - 7)\\ N = (- 5 x - 2)(-5 x + 2)\\ O = (2 + 4 x)(4 x - 2)\\ P = (x + 0,1)^2\\ Q = (0,2 y - 5)^2\\ R = (2 y - 0,3)(0,3 + 2 y)\\ S = (- 5 x + 2)^2\\ T = (4 + y)(y - 4))
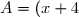^2) est de la forme (a + b)² avec a =
est de la forme (a + b)² avec a =  et b = 4. Donc :
et b = 4. Donc :
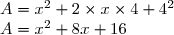
^2) est de la forme (a + b)² avec a = 5 et b =
est de la forme (a + b)² avec a = 5 et b =  . Donc :
. Donc :
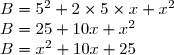
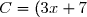^2) est de la forme (a + b)² avec a =
est de la forme (a + b)² avec a = 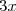 et b = 7. Donc :
et b = 7. Donc :
^2 + 2 \times 3 x \times 7 + 7^2\\ C = 9 x^2 + 42 x + 49)
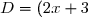^2) est de la forme (a + b)² avec a =
est de la forme (a + b)² avec a = 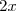 et b = 3. Donc :
et b = 3. Donc :
^2 + 2 \times 2 x \times 3 + 3^2\\ D = 4 x^2 + 12 x + 9)
^2) est de la forme (a + b)² avec a = 7 et b =
est de la forme (a + b)² avec a = 7 et b = 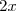 . Donc :
. Donc :
^2\\ E = 49 + 28 x + 4 x^2\\ E = 4 x^2 + 28 x + 49)
^2) est de la forme (a + b)² avec a = 3 et b =
est de la forme (a + b)² avec a = 3 et b = 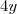 . Donc :
. Donc :
^2\\ F = 9 + 24 y + 16 y^2\\ F = 16 y^2 + 24 y + 9)
^2) est de la forme (a - b)² avec a =
est de la forme (a - b)² avec a =  et b = 2. Donc :
et b = 2. Donc :
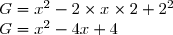
^2) est de la forme (a - b)² avec a =
est de la forme (a - b)² avec a = 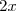 et b = 5. Donc :
et b = 5. Donc :
^2 - 2 \times 2 x \times 5 + 5^2\\ H = 4 x^2 - 20 x + 25)
^2) est de la forme (a - b)² avec a = 3 et b =
est de la forme (a - b)² avec a = 3 et b = 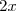 . Donc :
. Donc :
^2\\ I = 9 - 12x + 4x^2\\ I = 4x^2 - 12x + 9)
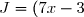^2) est de la forme (a - b)² avec a =
est de la forme (a - b)² avec a = 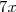 et b = 3. Donc :
et b = 3. Donc :
^2 - 2 \times 7x \times 3 + 3^2\\ J = 49x^2 - 42x + 9)
(x + 7)) est de la forme (a - b)(a + b) avec a =
est de la forme (a - b)(a + b) avec a =  et b = 7. Donc :
et b = 7. Donc :
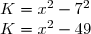
(2x + 3)) est de la forme (a - b)(a + b) avec a =
est de la forme (a - b)(a + b) avec a = 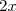 et b = 3. Donc :
et b = 3. Donc :
^2 - 3^2\\ L = 4x^2 - 9)
(3 x - 7)) est de la forme (a - b)(a + b) avec a =
est de la forme (a - b)(a + b) avec a = 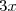 et b = 7. Donc :
et b = 7. Donc :
^2 - 7^2\\ M = 9x^2 - 49)
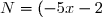(-5 x + 2)) est de la forme (a - b)(a + b) avec a =
est de la forme (a - b)(a + b) avec a = 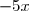 et b = 2. Donc :
et b = 2. Donc :
^2 - 2^2\\ N = 25x^2 - 4)
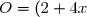(4 x - 2)\\ O = (4 x + 2)(4 x - 2)) est de la forme (a - b)(a + b) avec a =
est de la forme (a - b)(a + b) avec a = 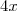 et b = 2. Donc :
et b = 2. Donc :
^2 - 2^2\\ O = 16x^2 - 4)
^2) est de la forme (a + b)² avec a =
est de la forme (a + b)² avec a =  et b = 0,1. Donc :
et b = 0,1. Donc :
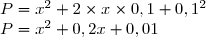
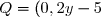^2) est de la forme (a - b)² avec a =
est de la forme (a - b)² avec a = 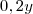 et b = 5. Donc :
et b = 5. Donc :
^2 - 2 \times 0,2y \times 5 + 5^2\\ Q = 0,04y^2 - 2y + 25)
(0,3 + 2y)\\ R = (2y - 0,3)(2y + 0,3)) est de la forme (a - b)(a + b) avec a =
est de la forme (a - b)(a + b) avec a = 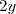 et b = 0,3. Donc :
et b = 0,3. Donc :
^2 - 0,3^2\\ R = 4y^2 - 0,09)
^2\\ S = (2 - 5 x)^2) est de la forme (a - b)² avec a = 2 et b =
est de la forme (a - b)² avec a = 2 et b = 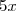 . Donc :
. Donc :
^2\\ S = 4 - 20x + 25x^2\\ S = 25x^2 - 20x + 4)
(y - 4)\\ T = (y + 4)(y - 4)) est de la forme (a - b)(a + b) avec a =
est de la forme (a - b)(a + b) avec a = 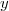 et b = 4. Donc :
et b = 4. Donc :
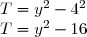 Publié par Océane
le
Publié par Océane
le
Identités Remarquables : Développement
Fiche relue en 2016.
Rappel : Identités remarquables
Pour tous les nombres  et
et  , on a :
, on a :
(a + b)² = a² + 2ab + b²
(a - b)² = a² - 2ab + b²
(a - b)(a + b) = a² - b²
(a + b)² = a² + 2ab + b²
(a - b)² = a² - 2ab + b²
(a - b)(a + b) = a² - b²
Remarques :
1. La lecture de ces résultats de gauche à droite comme écrit ci-dessus permettent de développer des produits.
Une lecture de droite à gauche permettrait de factoriser des expressions. Effectivement, on obtient alors :
a² - 2ab + b²=(a - b)²
a² - b²=(a - b)(a + b)
2. Devant une différence de deux termes qu'on a à factoriser, il sera bon de penser à l'identité remarquable
Exemple : factoriser x²-7 ; repérer que 7 est le carré de
3. Il est d'usage de présenter les résultats des développements sous forme ordonnée suivant les puissances d'une variable choisie.
Développer et réduire les expressions suivantes :
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter

 Voir l'énoncé seul
Voir l'énoncé seul