Fiche de mathématiques
Ile mathématiques > maths 3ème > Sujets de brevet
A =+(2+\sqrt{11}))
B =(2+\sqrt{11}))
C =(2\sqrt{3}+1))
D =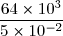
E =^2)
F =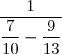
G =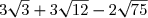
H =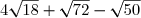
1. Développer E et réduire l'expression obtenue.
2. Factoriser E.
3. Résoudre l'équation (1 - 2x)(7 + 2x) = 0.
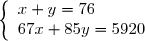
2. Un particulier achète 76 plants d'arbres fruitiers constitués de pommiers à 67 francs le pied et de poiriers à 85 francs le pied; le montant de la facture s'élève à 5920 francs.
a) Mettre le problème en équations.
b) Déterminer le nombre d'arbres fruitiers de chaque sorte.
A =^2)
B =(3\sqrt{2}+1))
C =^2+(2\sqrt{2}-3)(3\sqrt{2}+7))
D =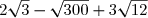
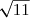 + 2 +
+ 2 + 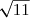
A = 2 + 2
A = 4
B = 2² -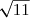 ² (identité remarquable)
² (identité remarquable)
B = 4 - 11
B = -7
C = (2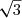 )² - 1² (identité remarquable)
)² - 1² (identité remarquable)
C = 2²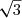 ² - 1
² - 1
C = 4×3 - 1
C = 12 - 1
C = 11
D =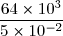
D =})
D =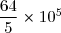
D = 12,8 × 105
D = 1,28 × 106
E = (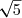 + 2)²
+ 2)²
E =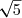 ² + 2 × 2
² + 2 × 2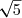 + 2² (identité remarquable)
+ 2² (identité remarquable)
E = 5 + 4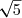 + 4
+ 4
E = 9 + 4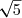
F =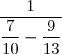
F =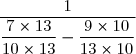 (on réduit au même dénominateur)
(on réduit au même dénominateur)
F =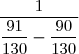
F =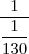
F = 130
G =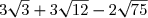
G = 3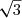 + 3
+ 3 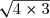 - 2
- 2 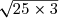
G = 3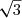 + 2 × 3
+ 2 × 3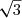 - 5 × 2
- 5 × 2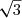
G = 3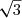 + 6
+ 6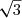 - 10
- 10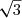
G = -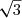
H =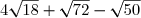
H =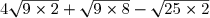
H =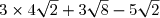
H =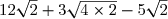
H =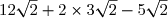
H =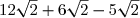
H =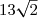
E = 16 - (2x + 3)²
E = 16 - [(2x)² + 2 × 3 × 2x + 3²]
E = 16 - 4x² - 12x - 9
E = -4x² - 12x + 7
2. Factorisons E : (identité remarquable)
E = [4 - (2x + 3)][4 + (2x + 3)]
E = (1 - 2x)(7 + 2x)
3. Résolvons E = 0 :
(1 - 2x) (7 + 2x) = 0
(1 - 2x) = 0 ou(7+2x) = 0
2x = 1 ou 2x = -7
x = ou x =
ou x = 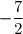
Les solutions de l'équation sont et
et 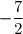 .
.
 \\ 67x + 85y = 5920 & (L_2) \\ \end{array} \right.)
 \\ 67x + 85y = 5920 & (L_2)\\ \end{array} \right.)
 \\ 67x + 85y = 5920 & (L_2)\\ \end{array} \right.)
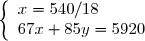
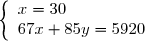

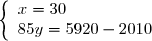
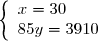
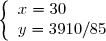
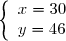
2. Soit x le nombre de pommiers
Soit y le nombre de poiriers
Il y a 76 plants d'arbres fruitiers en tout (pommiers + poiriers)
donc x + y = 76
Un pommier coûte 67 francs donc x pommiers coûtent 67x francs
Un poirier coûte 85 francs donc y poiriers coûtent 85y francs
Le prix total des x pommiers et des y poiriers est 5920 F
Soit 67x + 85y = 5920
On obtient le système
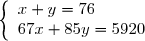
Dont les solutions sont :
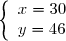
Il y a donc 30 pommiers et 46 poiriers.
 (identité remarquable)
(identité remarquable)
A =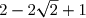
A =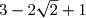
B =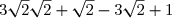
B =+1)
B =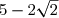
C = 4² + 2 × 4 × 5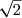 + (5
+ (5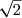 )² + 2 × 3 ×
)² + 2 × 3 × 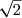
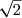 + 7 × 2
+ 7 × 2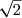 - 3 × 3
- 3 × 3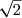 - 3 × 7
- 3 × 7
C = 16 + 40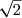 + 25 × 2 + 6 × 2 + 14
+ 25 × 2 + 6 × 2 + 14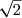 - 9
- 9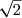 - 21
- 21
C = 57 + 45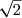
D = 2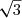 -
-  + 3
+ 3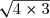
D = 2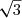 - 10
- 10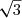 + 3 × 2
+ 3 × 2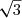
D = 2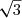 - 10
- 10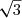 + 6
+ 6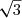
D = -2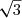 Publié par Tom_Pascal
le
Publié par Tom_Pascal
le
Exercices maison
exercice 1
Calculer les expressions suivantes:A =
B =
C =
D =
E =
F =
G =
H =
exercice 2
x étant un nombre, soit E = 16 - (2x + 3)²1. Développer E et réduire l'expression obtenue.
2. Factoriser E.
3. Résoudre l'équation (1 - 2x)(7 + 2x) = 0.
exercice 3
1. Résoudre le système:2. Un particulier achète 76 plants d'arbres fruitiers constitués de pommiers à 67 francs le pied et de poiriers à 85 francs le pied; le montant de la facture s'élève à 5920 francs.
a) Mettre le problème en équations.
b) Déterminer le nombre d'arbres fruitiers de chaque sorte.
exercice 4
Développer et réduire les expressions suivantes:A =
B =
C =
D =
exercice 1
A = 2 -A = 2 + 2
A = 4
B = 2² -
B = 4 - 11
B = -7
C = (2
C = 2²
C = 4×3 - 1
C = 12 - 1
C = 11
D =
D =
D =
D = 12,8 × 105
D = 1,28 × 106
E = (
E =
E = 5 + 4
E = 9 + 4
F =
F =
F =
F =
F = 130
G =
G = 3
G = 3
G = 3
G = -
H =
H =
H =
H =
H =
H =
H =
exercice 2
1. Développons E :E = 16 - (2x + 3)²
E = 16 - [(2x)² + 2 × 3 × 2x + 3²]
E = 16 - 4x² - 12x - 9
E = -4x² - 12x + 7
2. Factorisons E : (identité remarquable)
E = [4 - (2x + 3)][4 + (2x + 3)]
E = (1 - 2x)(7 + 2x)
3. Résolvons E = 0 :
(1 - 2x) (7 + 2x) = 0
(1 - 2x) = 0 ou(7+2x) = 0
2x = 1 ou 2x = -7
x =
Les solutions de l'équation sont
exercice 3
1. Résolution du système2. Soit x le nombre de pommiers
Soit y le nombre de poiriers
Il y a 76 plants d'arbres fruitiers en tout (pommiers + poiriers)
donc x + y = 76
Un pommier coûte 67 francs donc x pommiers coûtent 67x francs
Un poirier coûte 85 francs donc y poiriers coûtent 85y francs
Le prix total des x pommiers et des y poiriers est 5920 F
Soit 67x + 85y = 5920
On obtient le système
Dont les solutions sont :
Il y a donc 30 pommiers et 46 poiriers.
exercice 4
A =A =
A =
B =
B =
B =
C = 4² + 2 × 4 × 5
C = 16 + 40
C = 57 + 45
D = 2
D = 2
D = 2
D = -2
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter

 Voir la correction
Voir la correction