Fiche de mathématiques
Ile mathématiques > maths 3ème > Racines carrées
Fiche relue en 2016.
Prouver que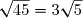 .
.
Prouver que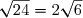 .
.
Mettre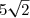 sous la forme d'une racine carrée.
sous la forme d'une racine carrée.
A=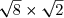
B=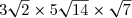
C=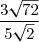
D=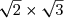
E=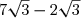
F=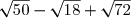
G=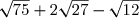
H=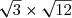
I=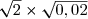
J=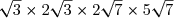
K=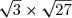
L=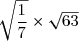
M=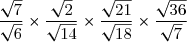
N=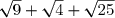
O=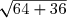
A= x²-2
B= 4x²-5
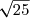 =
=
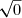 =
=
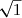 =
=
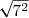 =
=
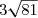 =
=
^2) =
=
^2) =
=
^2) =
=
^4) =
=
^6}) =
=
Le nombre étant positif,
étant positif, 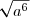
A=(\sqrt{7}+3))
B=^2)
C=^2)
D=^2)
E=(\sqrt{2}+5))
F=^2)
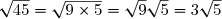
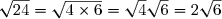
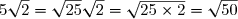
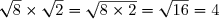
B=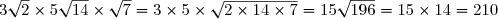
C=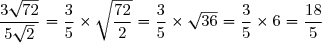
D=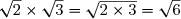
E=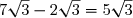
F=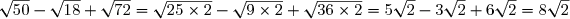
G=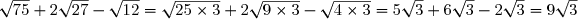
H=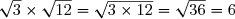
I=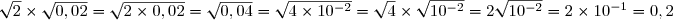
J=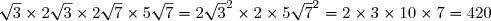
K=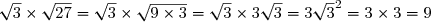
L=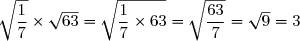
M=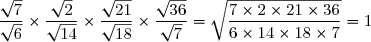
N=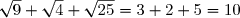
O=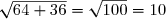
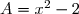
En remarquant que le nombre 2 peut s'écrire^2)
On reconnaît l'identité remarquable a² - b² = (a - b)(a + b) :
(x+\sqrt{2}))
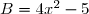
En remarquant que le nombre 5 peut s'écrire^2)
On reconnaît l'identité remarquable a² - b² = (a - b)(a + b) :
(2x+\sqrt{5}))
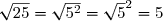
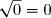
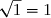
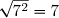
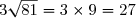
^2 = 5)
^2 = 3^2\times\sqrt{2}^2 = 9\times2 = 18)
^2 = (\sqrt{3})^2 = 3)
^4 = (\sqrt{5})^4 = \left((\sqrt{5})^2\right)^2 = 5^2 = 25)
^6} = \sqrt{2^6} = \sqrt{(2^3)^2} = 2^3 = 8)
^2} = a^3)
(\sqrt{7}+3))
On reconnaît l'identité remarquable (a + b)(a - b) = a² - b²
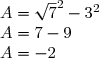
^2)
On reconnaît l'identité remarquable (a + b)² = a² + 2ab + b²
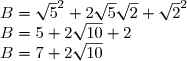
^2)
On reconnaît l'identité remarquable (a + b)² = a² + 2ab + b²
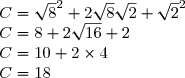
^2)
On reconnaît l'identité remarquable (a + b)² = a² + 2ab + b²
^2+2\times(3\sqrt{2})(2\sqrt{3})+(2\sqrt{3})^2\\D = 3^2\sqrt{2}^2 + 2\times3\times2\times\sqrt{2}\times\sqrt{3} + 2^2\sqrt{3}^2\\D = 9\times2+12\sqrt{6}+4\times3\\D = 18+12\sqrt{6}+12\\D = 30+12\sqrt{6})
(\sqrt{2}+5))
On reconnaît l'identité remarquable (a + b)(a - b) = a² - b²
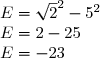
^2)
On reconnaît l'identité remarquable (a + b)² = a² + 2ab + b²
^2+2\times2\sqrt{3}+1^2\\F = 4\times3+4\sqrt{3}+1\\F = 13+4\sqrt{3}) Publié par Tom_Pascal
le
Publié par Tom_Pascal
le
Les racines carrées
Fiche relue en 2016.
exercice 1
Prouver que
Prouver que
Mettre
exercice 2
Calculer les expressions suivantes:A=
B=
C=
D=
E=
F=
G=
H=
I=
J=
K=
L=
M=
N=
O=
exercice 3
Factoriser les expressions suivantes:A= x²-2
B= 4x²-5
exercice 4
Ecrire sans radical les nombres suivants :Le nombre
exercice 5
Développer les produits suivants et simplifier-les si possible :A=
B=
C=
D=
E=
F=
exercice 1
exercice 2
A=B=
C=
D=
E=
F=
G=
H=
I=
J=
K=
L=
M=
N=
O=
exercice 3
En remarquant que le nombre 2 peut s'écrire
On reconnaît l'identité remarquable a² - b² = (a - b)(a + b) :
En remarquant que le nombre 5 peut s'écrire
On reconnaît l'identité remarquable a² - b² = (a - b)(a + b) :
exercice 4
exercice 5
On reconnaît l'identité remarquable (a + b)(a - b) = a² - b²
On reconnaît l'identité remarquable (a + b)² = a² + 2ab + b²
On reconnaît l'identité remarquable (a + b)² = a² + 2ab + b²
On reconnaît l'identité remarquable (a + b)² = a² + 2ab + b²
On reconnaît l'identité remarquable (a + b)(a - b) = a² - b²
On reconnaît l'identité remarquable (a + b)² = a² + 2ab + b²
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter

 Voir la correction
Voir la correction