Fiche de mathématiques
Ile mathématiques > maths 3ème > Racines carrées
Fiche relue en 2016.
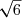 , avec a et b des entiers relatifs, le nombre suivant :
, avec a et b des entiers relatifs, le nombre suivant :
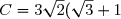 - ( \sqrt{2} + 1)(\sqrt{2} + 2))
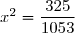
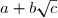 , où a et b sont des rationnels et c un entier naturel le plus petit possible.
, où a et b sont des rationnels et c un entier naturel le plus petit possible.
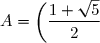^2 + 3)
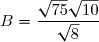
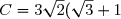 - ( \sqrt{2} + 1)(\sqrt{2} + 2)) (Développement)
(Développement)
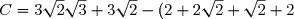) (Calcul de
(Calcul de 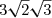 et retrait de la parenthèse)
et retrait de la parenthèse)
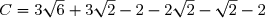 (On remarque que
(On remarque que 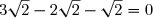 )
)
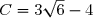
(Mise en forme pour répondre à la question)
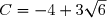
Donc a = -4 et b = 3
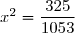
Remarque :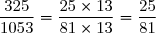
L'équation proposée peut donc s'écrire :
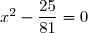
On reconnaît la différence de deux carrés que l'on factorise.
\left(x+\dfrac{5}{9}\right)= 0)
Un produit de facteurs est nul si l'un au moins de ses facteurs est nul, ce qui donne :
 ou
ou 
D'où l'ensemble solution peut s'écrire :
^2 + 3)
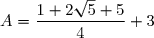 (Calcul du carré grâce à l'identité remarquable : (a+b)² = a² + 2ab + b²)
(Calcul du carré grâce à l'identité remarquable : (a+b)² = a² + 2ab + b²)
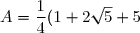 + \dfrac{1}{4} \times 12) (Recherche d'un dénominateur commun)
(Recherche d'un dénominateur commun)
 )
 )
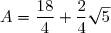 (Simplification)
(Simplification)
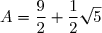 (Simplification)
(Simplification)
D'où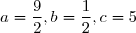
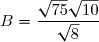
750 = 25 x 30 (25 étant le plus grand carré divisant 750)
8 = 4 x 2 (4 étant le plus grand carré divisant 8)


D'où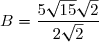
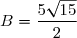
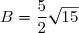
D'où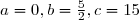
Publié par Tom_Pascal
le
Racines Carrées
Fiche relue en 2016.
Exercices d'application
exercice 1
Mettre sous forme a + bexercice 2
Déterminer les nombres réels x tels que :exercice 3
Ecrire sous le formeexercice 1
(Mise en forme pour répondre à la question)
Donc a = -4 et b = 3
exercice 2
Remarque :
L'équation proposée peut donc s'écrire :
On reconnaît la différence de deux carrés que l'on factorise.
Un produit de facteurs est nul si l'un au moins de ses facteurs est nul, ce qui donne :
D'où l'ensemble solution peut s'écrire :
exercice 3
D'où
750 = 25 x 30 (25 étant le plus grand carré divisant 750)
8 = 4 x 2 (4 étant le plus grand carré divisant 8)
D'où
D'où
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter

 Voir la correction
Voir la correction