Inscription / Connexion Nouveau Sujet
1ere spécialitétangentes et ciblés à atteindre dans un jeu vidéo
Bonjour, j'ai du mal avec mon Devoir maison de mathématiques, est ce possible d'avoir un coup de pouce s'il vous plaît ?
Voici l'énoncé :
Dans un jeu vidéo, un avion se déplace de gauche à droite sur une courbe de type hyperbole. Des cibles numérotées C 1 à C 8 sont placées sur l'axe des abscisses.
La cible C1 a pour abscisse 1, ..., la cible C8 a pour abscisse 8
Le joueur appuie sur une commande qui déclenche, depuis l'avion, un tir rectiligne dirigé selon la tangente à la trajectoire au moment du tir.
On sait que la trajectoire de l'avion a pour équation y = 2 + 2/x
pour x > 0. Cette courbe sera notée (C)
Partie A : Etude du tir dans 2 positions particulières de l'avion.
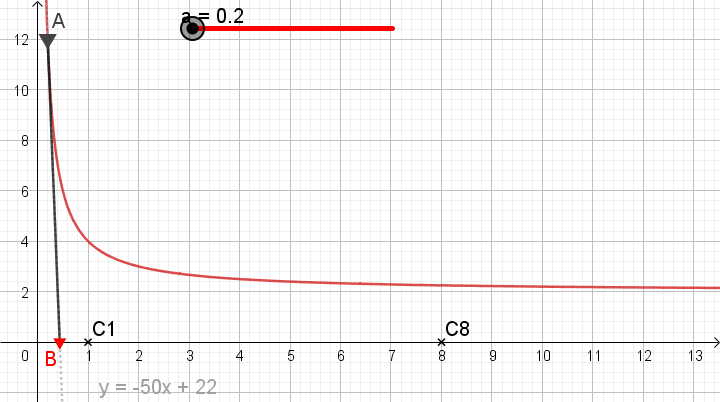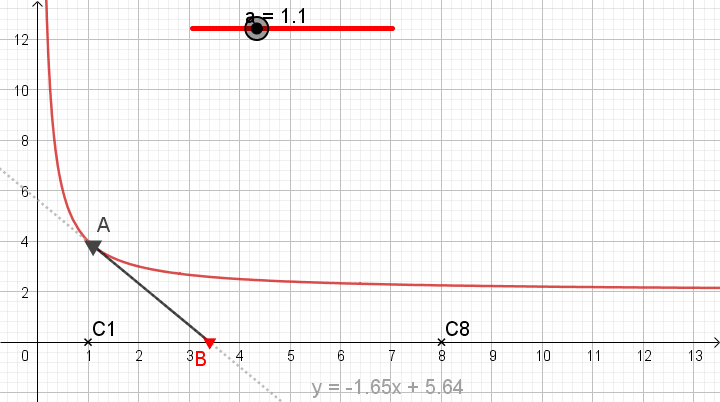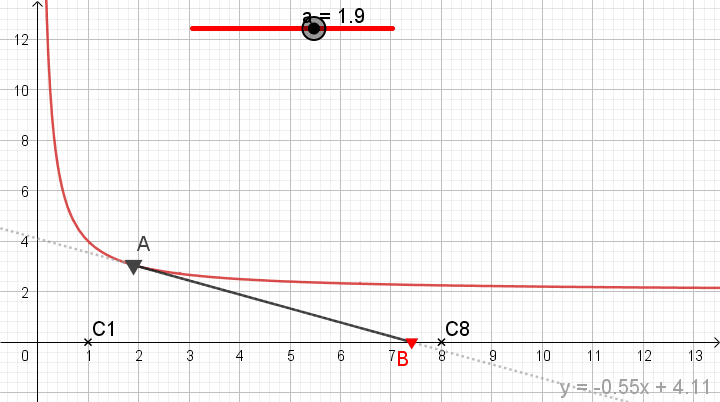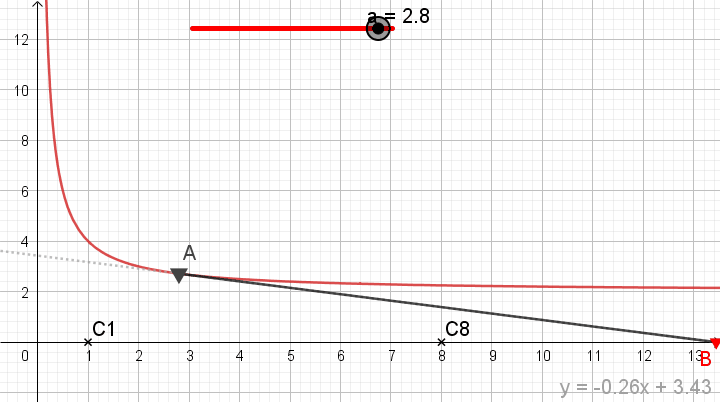
1) On note A le point d'abscisse 2 de la courbe (C) . Déterminer l'équation de la tangente à (C) au point A .
2) Prouver que lorsque l'avion passera en A il pourra atteindre une des cibles. On précisera laquelle.
3) On note B le point d'abscisse 1 de la courbe (C). Prouver que lorsque l'avion passera en B il pourra atteindre une des cibles. On précisera laquelle.
Pour la partie 1) j'ai trouvé ceci : y = -0,5x + 4
avec dérivable en 2 et son nombre dérivé vaut L = -0,5
Pour le reste je me suis dit que je devais remplacer x et y par des valeurs par exemple du point A donc ( a ; f(a) ) mais je n'en suis pas sure.
Je ne sais pas si c'est bon et je galère complètement pour la suite de l'exercice… je vous remercie d'avance pour votre réponse.
Bonjour
D'accord pour l'équation de la tangente en A.
En quel point va-t-elle couper l'axe des abscisses ?
super merci!
je pense que a = 2 et f(a)= 2+2/2= 3
je pense donc qu'elle va couper l'axe des abscisses au point C2 ?
Vous avez calculé ceci pour écrire l'équation de la tangente
On vous dit
Le joueur appuie sur une commande qui déclenche, depuis l'avion, un tir rectiligne dirigé selon la tangente à la trajectoire au moment du tir.
Ce qui signifie que la trajectoire du missile est la tangente. Il atteindra la cible située sur la droite tangente et sur l'axe des abscisses. Ce n'est donc pas C2
je crois que la réponse à la deuxième question est C8. Mais ainsi avec ce que vous me dites, je ne vois pas comment le prouver.. je dois utiliser y = -0,5x + 4 c'est ça ?
Oui, C8 je vous l'ai indiquée, vous résolvez le système formé par les équations des deux droites ici, le système est simplifié :
j'ai fait pour la question 2 :
0 = -0,5x + 4
-4 = -0,5x
x = 8
Sachant que la cible C8 a pour abscisse 8, l'avion atteindra cette cible quand il passera en A.
Pour la question 3, j'ai fait la même chose que la 1 et 2.
J'ai trouvé que l'équation de la tangente était y = -2x + 6 , puis que x = 3 ( toujours avec la même méthode ). Donc, si je ne me suis pas trompée, l'avion atteindra la cible 3 lorsqu'il passera en B ?
l'avion atteindra cette cible quand il passera en A.
Je préfèrerais : la cible atteinte lorsqu'il lancera son missile en A est C8.
Oui, La cible atteinte est C3
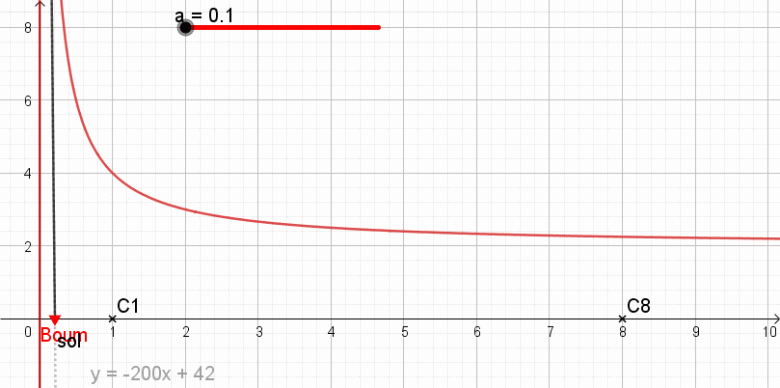
illustration
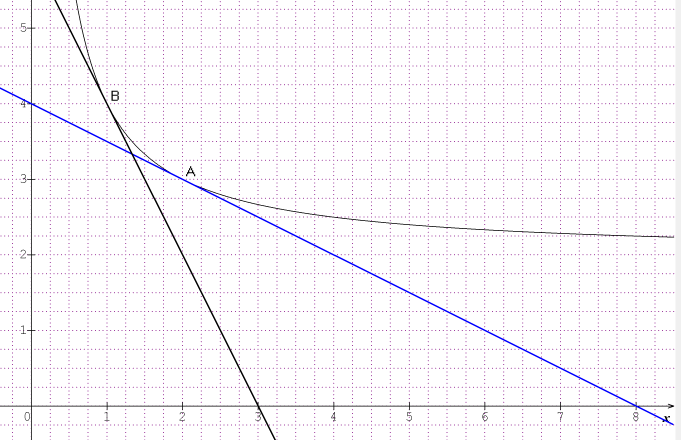
merci beaucoup pour votre aide! Je modifie tout ça.
J'ai également une deuxième partie, je ne sais pas si vous auriez le temps de m'aider, au cas où je mets la suite ici avec ce que j'ai fait :
Partie B : Etude du tir sur les cibles dans le cas général.
Soit a un réel > 0 donné. On note M le point d'abscisse a de la courbe (C).
1°) En utilisant la formule du cours pour l'équation d'une tangente montrer que la tangente à la courbe (C) au point M d'abscisse a, a pour équation: y = (- 2/a^2)*x + 2 + 4/a
2°) On note Ta le point d'intersection de la tangente précédente avec l'axe des abscisses.
a) Déterminer en fonction du réel a les coordonnées du point Ta.
b) Montrer qu'en prenant a = 1 puis a = 2 on retrouve les résultats de la partie A.
c) Déterminer l'abscisse exacte que doit posséder l'avion pour déclencher un tir qui atteindra la cible C 2.
Pour la question 1, j'ai fait :
avec : y = f'(a)*(x-a)+f(a)
on a : f(a)= 2+2/a et f'(a) = -2/a^2
y = f'(a)*(x-a)+f(a)
y = -2/a^2*(x-a) + 2 + 2/a
y = (-2/a^2)*x + (2/a^2)*a + 2 + 2/a
y = (-2/a^2)*x + 2*a/a^2+ 2 + 2/a
y = (-2/a^2)*x + 2 + 4/a
je suis maintenant à la deuxième question. Je ne suis pas sure de comprendre. On cherche bien les coordonnées sous cette forme là : A( a ; f(a) ) ?
Question 1 d'accord. Vous reprenez bien, les résultats de la première partie pour
le calcul de ce n'est pas la peine de la recalculer.
Question 2 a) résolution du système
b Vous avez donc obtenu une abscisse Quelle est-elle si vous donnez à
la valeur 1 puis la valeur 2. Normalement, vous devez retrouver les résultats de la partie précédente.
c) Pour quelle valeur de le système admet-il pour solution
voici ce que j'ai commencé pour le a)
0=(-2/a^2)*x + 2 + 4/a
-2 = (-2/a^2)*x + 4/a
-2-4/a = (-2/a^2)*x
-2a/a - 4/a = (-2/a^2)*x
je suis bloquée à ici, je ne sais pas quoi faire.. je dois peut être simplifier d'un côté ?
j'ai continué mon calcul et j'ai trouvé x = a^2 + 2a
je pense que c'est bon, je n'écris pas mon calcul car il est plutôt long et avec beaucoup de divisions
Oui, c'est bien ce résultat
on multiplie d'abord tout par
on divise par 2 :
d'où Pourquoi plein de division ?
ou directement
effectivement beaucoup plus simple, je n'ai pas procédé de la même façon ^^'! J'ai continué sur ma lancée donc un calcul à rallonge..
pour la dernière partie j'ai ça :
a^2 + 2a = 2
a^2 + 2a - 2 = 0
a = (-2 ± √(2^2 - 4 * 1 * -2)) / (2 * 1)
a = (-2 ± √(4 + 8)) / 2
a = (-2 ± √12) / 2
a = (-2 ± 2√3) / 2
a = -1 ± √3
Donc, les solutions de l'équation sont a = -1 + √3 et a = -1 - √3.
Je ne sais pas si il y a une manière plus simple de résoudre ici
Oui, ce sont bien les solutions de l'équation .
Vous n'avez pas conclu.
O peut dire : équation du second degré
2 sol