Inscription / Connexion Nouveau Sujet
1s devoir nombre dérivé
Bonjour j'ai un Devoir Maison à rendre vendredi et je ne comprend rien à l'exercice.
voici la consigne:
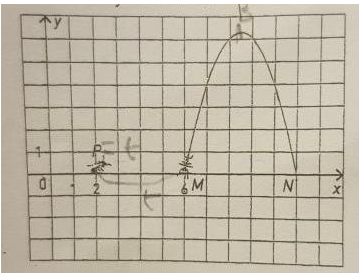
Une fourmi se déplace sur un arceau du point M vers le point N. On suppose qu'on néglige la longueur de la fourmi.
L'arceau a la forme d'une parabole d'équation : y= -x2+17x-66
Une cigale est placée en P de coordonnées (2; 0)
On appelle a l'abscisse de la fourmi.
A partir de quelle valeur de a la cigale ne verra-t-elle plus la fourmi ?
Merci de m'aider le plus rapidement possible.
Bonsoir, commence par dessiner la parabole et comprend ce que l'on demande.
tu vois bien que la cigale ne verra plus la fourmi quand elle aura dépassé le point de tangence de la droite tangente menée de P à la parabole. Donc trouve le.
en plus ils te font le dessin ... ils sont gentils !
trace (même de façon approximative pour se faire une idée) la tangente à la parabole passant pas P
elle est tangente à la parabole en un point d'abscisse a
si l'abscisse de la fourmi est inférieure à a, la cigale la voit
et ne la verra plus dès que l'abscisse de la fourmi sera supérieure à a
Enfin je me suis mal exprimé j ai compris le principe de l exercice mais je ne comprend pas comment l y prendre pour n expliquer mathématiquement je ne sais pas par où commencer et comment
ben à ton avis ? on va pas utiliser une tronçonneuse 
et tu traduis que cette tangente doit passer par le point P
tu as écrit l'équation de la tangente... alors traduis le fait que cette droite passe par le point P
bon alors ,
c'est quand même pas compliqué d'écrire que la droite d'équation y=f'(a)(x-a) + f(a) passe par le point (2;0) ...
Bah enfaite je sais que je dois trouve f(a+h) et f(a) puis le taux d accroissement qui me donne f'(a) mais je sais pas comment trouver f(a+h) et f(a) en fonction de mon sujet justement
si tu ne comprends pas ce que je demande à 18:55 c'est un vrai problème !
traduire qu'une droite passe pas un point est vu en troisième et en seconde