Inscription / Connexion Nouveau Sujet
3 points sur une hyperbole
Bonjour
après ![]() deux points sur une hyperbole et en "révisant" mon livre de terminale sur le sujet j'y ai trouvé l'exercice suivant :
deux points sur une hyperbole et en "révisant" mon livre de terminale sur le sujet j'y ai trouvé l'exercice suivant :
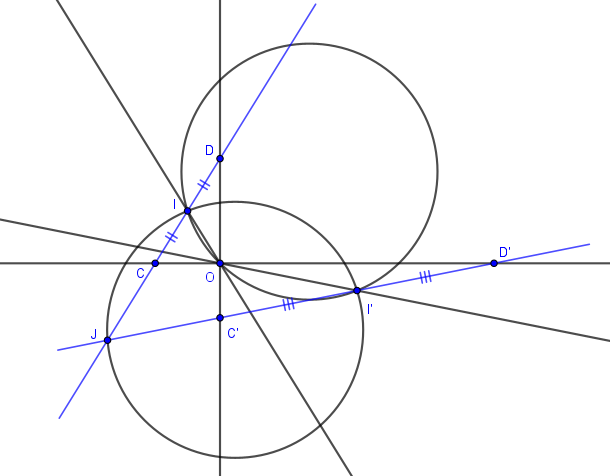
Soit une hyperbole équilatère [de centre O] et deux droites qui coupent les asymptotes, l'une en A et B et l'autre en A' et B'
1° soit I le milieu de AB et I' le milieu de A'B'. Comparer les angles de droite (modulo  ) (OI, OI' ) et (AB, A'B' )
) (OI, OI' ) et (AB, A'B' )
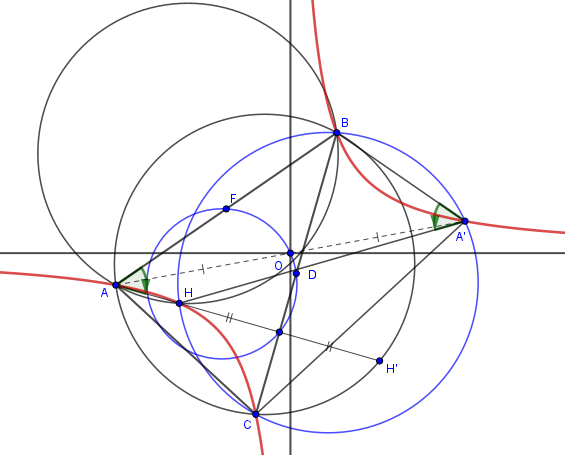
2° en déduire que si un triangle ABC est inscrit dans une hyperbole équilatère de centre O :
a) le cercle d'Euler du triangle ABC passe par O
b) l'orthocentre du triangle ABC est sur l'hyperbole
je rajoute :
c) que peut en dire du 4ème point d'intersection M de l'hyperbole et du cercle circonscrit à ABC ?
Nota : je n'ai pas tout "niveau terminale", je cherche encore la preuve "élémentaire" du 2b), j'y ai utilisé de la géométrie projective ...
de plus je ne suis pas d'accord avec la conclusion !
comme tu as blanqué, je blanque aussi :
 Cliquez pour afficher
Cliquez pour afficherBonjour,
je réponds à la question 2b, elle n'utilise que la définition de l'othocentre (intersection des hauteurs) :
 Cliquez pour afficher
Cliquez pour afficheroui, en ajoutant les définitions de tout ça ;
sans perte de généralité on peut supposer que l'hyperbole a pour équation xy = 1
et les points A (a; 1/a), B (b; 1/b) et C(c; 1/c)
ce calcul s'avère finalement le plus direct !
mais n'a aucun rapport avec ce que suggère l'énoncé par "en déduire".
il aurait donc dû être
2a) en déduire que O est sur le cercle d'Euler
2b) justifier (indépendamment, et pas "en déduire") que H est sur l'hyperbole
joli !
"le théorème du LH" ? du Lebossé-Hémery ?
en fait c'est une sorte de réciproque de la question 1.
(d'où le fait que c'est bien "en déduire")
Oui, le Lebossé & Hémery; voici la page en question :

En fait, j'avais trouvé ton énoncé dans le tome Géométrie/mécanique du cours Maillard Girard et Lentin (n°747 page 400 dans mon édition de 1964).
Mais rien de bien concluant dans le cours correspondant. 
Au sujet du LH, je peux peut-être te venir en aide.
Si (et seulement si !)tu es intéressé, mon adresse mail est dans mon profil 
Vu,
comme ce sont des propriétés "classiques" il est logique que ça apparaisse dans diverses sources, sous des formes seulement légèrement différentes.
Bonjour,
Autre solution où la réciproque du 1) est utilisée sans théorèmes du LH (peut-être plus adaptée au Maillard) :
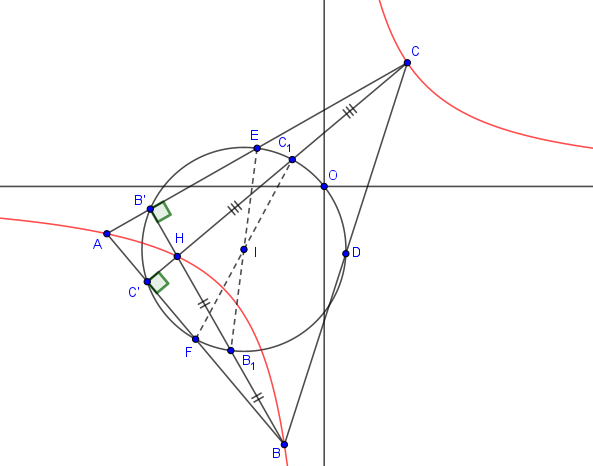
En angles orientés de droites donc modulo :
(angles de droites perpendiculaires).
(application du 1) où
et
sont confondus).
(les points
et
d'une part,
et
d'autre part sont diamétralement opposés sur le cercle d'Euler)
On a donc qui prouve que
appartient à l'hyperbole avec la réciproque du 1).
La troisième égalité est immédiate avec Chasles et une somme nulle d'angles orientés modulo
:
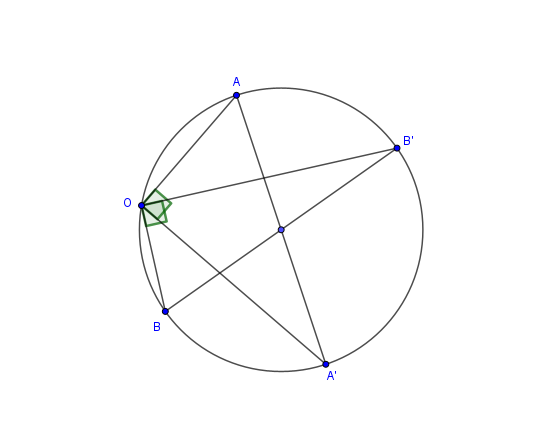
Dans tous les cas de figure,
Bonjour,
c'est très certainement du genre de ce qui était attendu dans le Maillard
de même la question1 se résout avec juste Chasles sans faire intervenir tes "cercles égaux" mais les triangles isocèles formés par la médiane d'un triangle rectangle.
je n'ai pas réussi à extraire le LaTeX de Geogebra pour le coller ici : il me dit erreur de LaTeX
même en refabriquant de toute pièce la même formule dans l'éditeur de l'ile, apparemment le \begin{align*} ne lui convient pas du tout
Oui, le du forum est "limité". L'environnement {align} ne passe pas.
Un fil qui date presque de 10 ans où il n'était question que du de la zone contribution un peu plus élaboré que celui du forum :
![]() Le LaTeX de la zone de contribution.
Le LaTeX de la zone de contribution.
Je n'y connais pas grand chose mais j'avais retenu que les choses sont extrêmement compliquées.
Pour notre hyperbole équilatère, j'étais convaincu que le premier jet pour 2)b) (avec le théorème du LH) n'était pas ce qui était attendu par le Maillard. J'ai mis "un certain temps" pour pondre 14h41.
En temps limité j'aurais été archi cuit ... 
salut,
je ne sais si ce code peut vous être utile
\begin {aligned}
\int_0^1\dfrac{x}{x+1}\;\mathrm {d}x &= \int_0^1\dfrac{x+1-1}{x+1}\;\mathrm {d}x
&= \int_0^1 1\;\mathrm {d}x-\int_0^1\dfrac{1}{x+1}\;\mathrm {d}x
&=\left[x\right]_0^1-\left[\ln(x+1)\right]_0^1
&=1-\ln2
\end {aligned}