Inscription / Connexion Nouveau Sujet
aire
Bonjour, voici un dernier exercice :
On note f la fonction définie sur R par : f(x)=(x+3)²(3-x)
1- a) Calculez f'(x)
b) Etudiez les variations de f
c) Lorsque x décrit l'intervalle [0;3], donnez un encadrement de f(x).
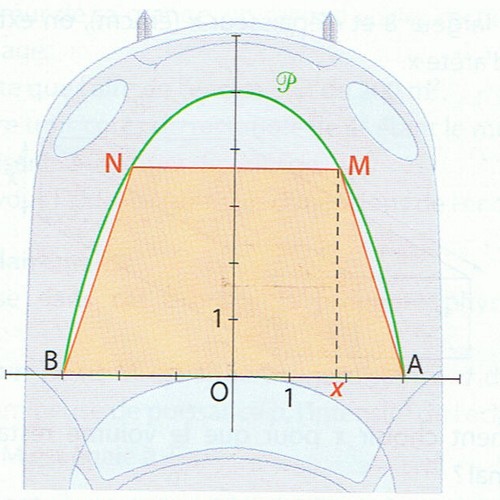
2- Un fabriquant d'accessoires de tuning veut produire des autocollants pour le capot de certains modèles de voitures. Il souhaite que l'image, trapézoïdale, ait la plus grande surface possible. Dans un repère orthonormé, P est la parabole d'équation y=(9-x²)/2. A et B sont les points de P de coordonnées respectives (3;0) et (-3;0). M et N sont les ponts de P d'abscisses respectives x et -x avec 0 x
x 3
3
a) Déterminez la valeur de x pour laquelle l'aire du trapèze AMNB est minimale.
j'ai fait :
1- a) (x²+6x+9)(3-x)=3x²-x3+18x-6x²+27-9x=-x3-3x²+9x+27 donc f'(x)=-3x²-6x+9
b) donc la fonction est croissante sur ]- ;-1[ et décroissante sur ]-1;+
;-1[ et décroissante sur ]-1;+ [
[
c) f(x)dans cet intervalle est compris entre -4 et 32
le reste je ne sais pas
Bonjour,
1)a) C'est ok pour le calcul de la dérivée.
b) Es-tu sûr des variations de f ? As-tu bien calculé les racines de la dérivée de f' ? J'ai un petit doute...
Tu as :
Discriminant :
Donc il y a 2 racines distinctes x1 et x2 que je laisse chercher.
Puis tu peux ensuite étudier le signe de f', puis les variations de f.
Je te laisse revoir correctement tes calculs, sachant qu'après bien sûr c'est faux aussi. (Je parle de ta réponse à la question 1)c)).
x1=1 et x2=-3
f' est négative donc croissante sur ]- ;12]et décroissante sur [12;+
;12]et décroissante sur [12;+ [ et pour les variations de f j'ai regardé sur la calculatrice
[ et pour les variations de f j'ai regardé sur la calculatrice
Es-tu sûr de ça ?? Des fois, il faut plus avoir confiance en soi-même qu'en sa calculatrice.  (La calculatrice te sert à vérifier tes calculs)
(La calculatrice te sert à vérifier tes calculs)
Reprenons les calculs, en effet tu trouves 2 racines distinctes qui sont : x1=-3 et x2=1.
Par conséquent, dans ton cours, lorsqu'il y a 2 racines distinctes x1 et x2, que peux-tu dire du signe de f' ? (Signe de a l'extérieur des racines, signe de -a à l'intérieur doit te rappeler sûrement des choses...)
j'ai vu ça dans mon cours (votre réponse entre parenthèse) mais le signe d'une dérivée ne me dit rien, c'est la même chose non ?
Tu trouves que f' admet 2 racines distinctes qui sont : x1=-3 et x2=1.
D'après le cours, lorsqu'il y a 2 racines distinctes x1 et x2, f' est du signe de a à l'extérieur des racines et de -a à l'intérieur des racines.
Dans notre exercice, a=-3<0, par conséquent :
f' est négatif à l'extérieur des racines x1 et x2.
f' est positif à l'intérieur des racines x1 et x2.
D'où le tableau de variations suivant : (Je te laisse en déduire les variations de f)
Tu n'as jamais tracé de tableau de variations ??
Les variations de f se déduisent du signe de f', on les représente avec des flèches montantes ou descendantes pour dire si f est croissante ou bien décroissante.
Ici, sur les intervalles ]-inf;-3] et [1;+inf[, f' est négatif. Donc f est décroissante sur ces intervalles.
Puis, sur l'intervalle [-3;1], f' est positif. Donc f est croissante sur cet intervalle.
Par ailleurs, je l'ai dit plus haut, dans la question 1)b), ton encadrement de f(x) est faux !
Tu le verras sur ton tableau de variations une fois complété.
Tu pourras calculer éventuellement f(0), f(1) et f(3) pour connaître l'encadrement de f(x).
2) La question est assez délicate. Je vais te donner un début de piste.
Tout d'abord, commences par calculer l'aire du trapèze AMNB en fonction de x.
(Je te rappelle tout de même la formule pour calculer l'aire d'un trapèze si tu l'aurais oublié : où B désigne la grande base du trapèze, b la petite base du trapèze et h la hauteur du trapèze.
ok la b) je la ferai plus tard
2) A=1/2(B+b).h donc 1/2(6+4).y=5y ? mais y on peut l'avoir avec f'(x) non ?
Attention, ce n'est pas tout à fait correct.
Tu as :
Selon le graphe, on a : AB=6, MN=2x (en effet la distance entre l'axe des ordonnées et le point M (ou N) est égale à x)
Ainsi :
.
Puis tu remplaces y par l'équation de ta parabole donnée en hypothèse.
C'est correct, mais tu peux faire plus simplement ! Tu as :
et tu reconnais que 9-x² est une identité remarquable.
Ainsi :
.
Et là, qu'est-ce tu ne remarques pas une relation de cette aire avec la fonction f du début de l'énoncé ? 
si on retrouve la première formule de l'énoncé alors je peux remettre la dérivée en la divisant par 2 ?


