Inscription / Connexion Nouveau Sujet
Aire d'un Triangle
Salut à tous, J'ai un dm à rendre pour la rentrée avec comme consigne de ma professeur d'utiliser le produit scalaire mais le problème c'est que je n'y arrive pas du tout ! J'ai vu que cet exercice a déjà été une fois résolu il y a longtemps mais le problème c'est qu'on a pas utilisé le produit scalaire. Bref, voilà le sujet  :
:
On donne dans le repère orthonormé ( O;  ;
;  ),
),
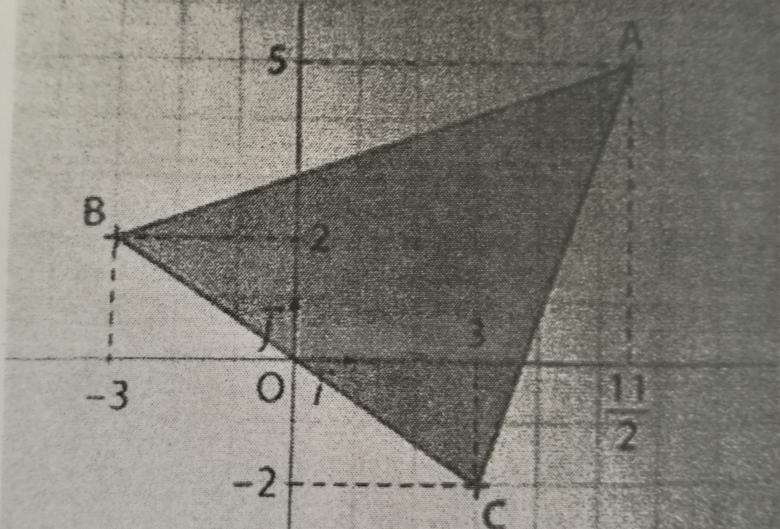
les points A ( 11/2 ; 5 ) B ( -3; 2 ) et C ( 3 ; -2).
Quelle est l'aire du triangle ABC ? ( J'ai joint le triangle en question afin que vous puissiez mieux comprendre )
Merci à vous !
Bonjour,
Vous pouvez tracer une des hauteurs du triangle, voir la formule et essayer de voir ce que ça donne avec les produits scalaires.
Bonjour,
pour calculer l'aire autrement qu'en faisant des découpages évidents (un rectangle moins trois triangles rectangles) on peut utiliser la formule classique de l'aire d'un triangle
1/2 base × hauteur
et c'est justement pour trouver cette hauteur qu'on va faire intervenir le produit scalaire :
en utilisant que si par exemple AH est la hauteur issue de A on a
à toi de traduire ça sur les coordonnées de H etc...
par exemple, appeler x et y les coordonnée de H
écrire le produit scalaire
écrire que H est sur BC (colinéarité)
résoudre ce système
une fois les coordonnée de H obtenues :
mesures de BC et AH et c'est quasiment fini
évidemment ce sera bien plus compliqué que la méthode de base avec les triangles rectangles, mais c'est "avec produit scalaire"
une autre méthode "avec produit scalaire" consiste à calculer le produit scalaire qui va donner le cosinus de l'angle A
puis l'aire sera 1/2 AB.AC sin A (car la hauteur issue de B est AB.sinA)
sans d'avantage de précisions de la part du prof on ne peut que deviner la méthode attendue par le prof sans jamais avoir de certitude que c'est celle qu'il attendait
(et peut être y en a-t-il encore d'autres ...)
Rony59, inscrit aujourd'hui et déjà 2 comptes, ce qui est complètement interdit, donc tu fermes l'autre tout de suite, pour retrouver la liberté avec celui-ci
j'attends que tu le fasses (connecte toi avec l'autre compte, va dans espace membre, puis désinscription)
edit > bon, y en a des qui comprennent le Français....on expliquera donc désormais à Sercan77350


