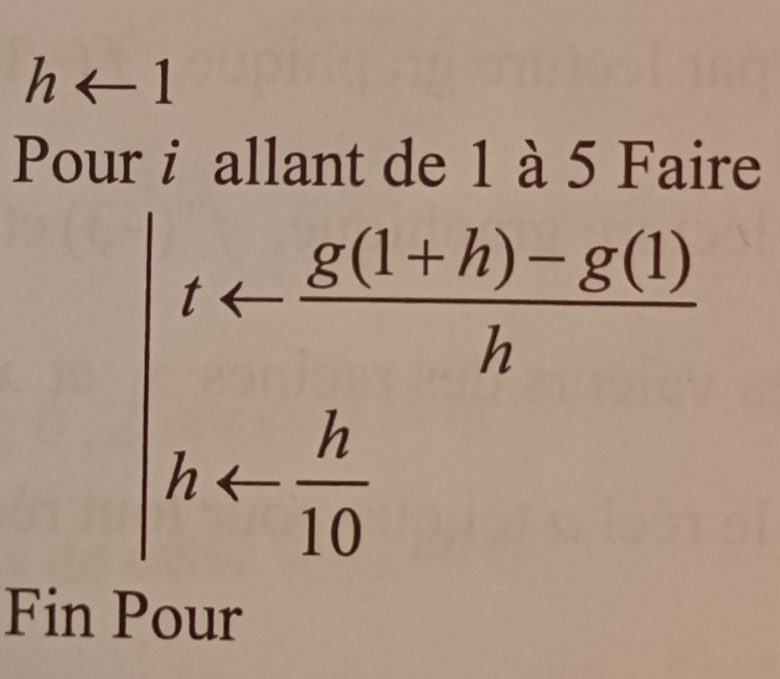Inscription / Connexion Nouveau Sujet
Algo
Bonjour j'ai g(x)= 1/2x-1
Que peut-on conjecturer en termes de dérivabilité ?
Je ne comprends pas la question

pour écrire g(x), tu dois donc utiliser des parenthèses
g(x)= 1 / (2x-1)
donne ton énoncé complet et exact (pas en photo !).. Quel est le rôle de l'algo par exemple ?
Soit la fonction definie par g(x)= 1/(2x-1).
Ci- contre algo.. en language courant:
On donne le tableau d'etat ci dessous en exécutant pas a pas l'algorithme.
J'ai calculé t pour i =5
Mais c'est la question 2 que je comprends pas
Oui moi aussi quand j'y pense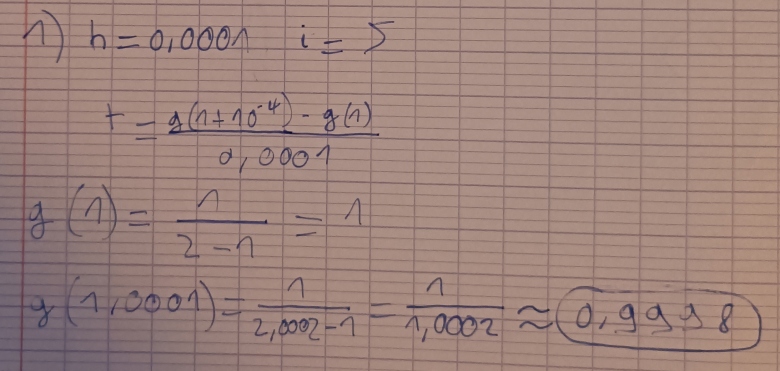
* Modération > Image exceptionnellement tolérée. Les brouillons doivent être recopiés. *
jusque là, c'est bon, mais tu n'es pas allé au bout
g(1,00001) = 0,9998 OK
g(1)=1 OK
t = ( g(1,00001) - g(1) ) / h = ??
erreur de signe, et arrondi un peu sauvage.. 
0,9998 - 1 est négatif.
donc tu obtiens plutôt - 1,9996
pour la question posée : est ce juste comme tu l'as écrite ? ou bien est ce qu'on précise "en termes de dérivabilité au point d'abscisse 1", par exemple ?
0,9998-1=-0,0002
-0,0002/0,0001= -2
Et "Que peut-on conjecturer en termes de dérivabilité pour la fonction g?"
Je pense que c'est 1
je t'ai écrit "donc tu obtiens plutôt - 1,9996 " quand tu ne fais pas d'arrondi au fur et à mesure du calcul..
pour i=5, t = -1,9996
ensuite :
" "Que peut-on conjecturer en termes de dérivabilité pour la fonction g?"
Je pense que c'est 1" ===> que veux tu dire ? "c'est 1" ? qu'est ce qui est 1 ?
tu peux conjecturer que g(x) est dérivable en 1 par exemple. A ton avis, à quoi correspondent les calculs que tu as fait dans ce tableau ? et à partir de là, qu'est ce qui te permet de conjecturer qu'elle est dérivable en 1 ?
et à ton avis, que vaudra le nombre dérivé en 1 noté g'(1) ?
Aah
Plus h tend vers 0 plus t = -2
Donc la fonction semble etre derivable quand a = 1 et le nombre dérivé est
g'(1)= -2
oui, c'est ça !
quand h tend vers 0, alors t tend vers -2
la limite de t quand h tend vers 0 est un nombre réel (limite finie), donc g(x) semble etre dérivable en 1 et on peut conjecturer que g'(1)=-2.
Parfait !
tu as d'autres questions ?