il faut faire une boucle  tant que b-a>p

Voilà, j'ai fait la boucle tant que:
1   VARIABLES
2     p EST_DU_TYPE NOMBRE
3     a EST_DU_TYPE NOMBRE
4     b EST_DU_TYPE NOMBRE
5     m EST_DU_TYPE NOMBRE
6     fa EST_DU_TYPE NOMBRE
7     fm EST_DU_TYPE NOMBRE
8   DEBUT_ALGORITHME
9     p PREND_LA_VALEUR 0.000001
10    LIRE a
11    LIRE b
12    TANT_QUE (b-a>p) FAIRE
13      DEBUT_TANT_QUE
14      m PREND_LA_VALEUR (a+b)/2
15      fa PREND_LA_VALEUR (2*a-1)/(a*a+2*a-2)
16      fm PREND_LA_VALEUR (2*m-1)/(m*m+2*m-2)
17      SI (fa*fm<=-5) ALORS
18        DEBUT_SI
19        b PREND_LA_VALEUR m
20        FIN_SI
21        SINON
22          DEBUT_SINON
23          a PREND_LA_VALEUR m
24          FIN_SINON
25      FIN_TANT_QUE
26    AFFICHER "la valeur de x est entre "
27    AFFICHER a
28    AFFICHER "et"
29    AFFICHER b
30  FIN_ALGORITHME

Résultats
***Algorithme lancé***
Entrer a : -7
Entrer b : 7
la valeur de x est entre 6.9999992et7
***Algorithme terminé***
Mais les résultats sont aussi faux...

si f est croissante

il faut affecter m puis f(m)
si f(m)<-5
ma
si f(m)>-5
mb

D'accord, mais si f est décroissante (et c'est le cas de cette fonction), on fait comment?

Bonjour,

un tel algorithme ne fonctionne que si la fonction est monotone et continue entre les valeurs initiales de a et b
et si f(a) et f(b) sont "de part et d'autre" de la cible
ce qui n'est pas le cas de cette fonction dans l'intervalle [-7; 7] : elle n'y est pas continue !!

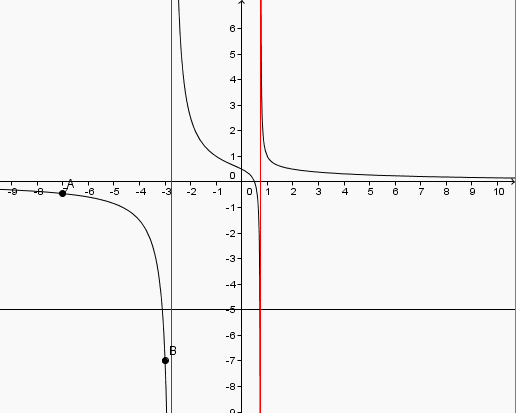
noter les asymptotes en x = -1 3 (valeurs interdites) et donc on ne peut choisir a et b que dans une même zone
ici dans ]-; -1-3[

la ligne
17 SI (fa*fm<=-5) ALORS
ne rime à rien du tout.

c'est (fa+5)*(fm+5) dont il faut tester le signe.

il faut étudier au préalable les variations de la fonction pour avoir au départ les intervalles [a; b] initiaux qui vont bien. voir ci-dessus

moyennnant quoi, en modifiant le SI et en partant de a = -7 et b = -3, et en se contentant d'une précision de 0.01 :

***Algorithme lancé***
Entrer a : -7
Entrer b : -3
a = -5, b = -3
a = -4, b = -3
a = -3.5, b = -3
a = -3.25, b = -3
a = -3.125, b = -3
a = -3.125, b = -3.0625
a = -3.125, b = -3.09375
a = -3.109375, b = -3.09375
a = -3.109375, b = -3.1015625
fini a = -3.109375, b = -3.1015625
***Algorithme terminé***

j'ai ajouté un affichage de a et b dans la boucle pour mieux voir les valeurs successives de a et b

D'accord, j'ai donc modifié mon algorithme comme vous me l'avait conseillé, mais les résultats ne changent pas, je ne comprends pas...
1   VARIABLES
2     p EST_DU_TYPE NOMBRE
3     a EST_DU_TYPE NOMBRE
4     b EST_DU_TYPE NOMBRE
5     m EST_DU_TYPE NOMBRE
6     fa EST_DU_TYPE NOMBRE
7     fm EST_DU_TYPE NOMBRE
8   DEBUT_ALGORITHME
9     p PREND_LA_VALEUR 0.000001
10    LIRE a
11    LIRE b
12    TANT_QUE (b-a>p) FAIRE
13      DEBUT_TANT_QUE
14      m PREND_LA_VALEUR (a+b)/2
15      fa PREND_LA_VALEUR (2*a-1)/(a*a+2*a-2)
16      fm PREND_LA_VALEUR (2*m-1)/(m*m+2*m-2)
17      SI ((fa+5)*(fm+5)<-5) ALORS
18        DEBUT_SI
19        a PREND_LA_VALEUR m
20        FIN_SI
21        SINON
22          DEBUT_SINON
23          b PREND_LA_VALEUR m
24          FIN_SINON
25      FIN_TANT_QUE
26    AFFICHER "la valeur de x est entre "
27    AFFICHER a
28    AFFICHER "et"
29    AFFICHER b
30  FIN_ALGORITHME

Résultats
***Algorithme lancé***
Entrer a : -7
Entrer b : -3
la valeur de x est entre -7et-6.999999
***Algorithme terminé***

le signe de (fa+5)(fm+5)

la ligne correcte est
SI ((fa+5)*(fm+5)<=0) ALORS

D'accord, merci!
Est-ce que les résultats vous paraissent cohérents?
VARIABLES
2     p EST_DU_TYPE NOMBRE
3     a EST_DU_TYPE NOMBRE
4     b EST_DU_TYPE NOMBRE
5     m EST_DU_TYPE NOMBRE
6     fa EST_DU_TYPE NOMBRE
7     fm EST_DU_TYPE NOMBRE
8   DEBUT_ALGORITHME
9     p PREND_LA_VALEUR 0.01
10    LIRE a
11    LIRE b
12    TANT_QUE (b-a>p) FAIRE
13      DEBUT_TANT_QUE
14      m PREND_LA_VALEUR (a+b)/2
15      fa PREND_LA_VALEUR (2*a-1)/(a*a+2*a-2)
16      fm PREND_LA_VALEUR (2*m-1)/(m*m+2*m-2)
17      SI ((fa+5)*(fm+5)<=0) ALORS
18        DEBUT_SI
19        a PREND_LA_VALEUR m
20        FIN_SI
21        SINON
22          DEBUT_SINON
23          b PREND_LA_VALEUR m
24          FIN_SINON
25      FIN_TANT_QUE
26    AFFICHER "la valeur de x est entre "
27    AFFICHER a
28    AFFICHER "et"
29    AFFICHER b
30  FIN_ALGORITHME

Résultats
***Algorithme lancé***
Entrer a : -7
Entrer b : -3
la valeur de x est entre -7et-6.9921875
***Algorithme terminé***

en fait il faut comprendre ça comme la résolution de g(x) = f(x) + 5 = 0
et on teste bien "comme d'hab" le signe de g(a)*g(m)
c'est à dire si g(a) et g(m) sont de signe contraire
(en supposant que les valeurs de départ sont g(a) et g(b) de signe contraire, sinon ça ne marche pas)

par exemple, pour trouver l'autre racine il faudrait prendre a = -2 ou 0 par exemple et b tellement près de -1+3 que l'on doit dès le départ partir de b = pas un entier : b = 0.73 par exemple

ce qui donne (sans rien changer à l'algo, juste les valeurs de départ saisies) :
***Algorithme lancé***
Entrer a : 0
Entrer b : 0.73
a = 0.365, b = 0.73
a = 0.5475, b = 0.73
a = 0.6387499999999999, b = 0.73
a = 0.684375, b = 0.73
a = 0.7071875, b = 0.73
a = 0.7071875, b = 0.7185937499999999
a = 0.7071875, b = 0.712890625
fini a = 0.7071875, b = 0.712890625
***Algorithme terminé***

pourquoi diantre as tu interverti le contenu du SI SINON par rapport à ton algo de départ ??? c'était bon ! sauf que c'était le signe qu'il fallait tester au lieu de ce que tu avais écrit !!!
bien sur que ton dernier résultat est faux !

si tu échanges le SI / SINON, il faut aussi remplacer le <= par >=

Ahhh d'accord, j'ai compris, merci
Ah oui, je suis désolée, j'ai pas fait attention...
Merci d'avoir pris le temps de m'expliquer, même si je suis longue à la détente... :/
Je vous souhaite une bonne fin de journée!
Au revoir.