Inscription / Connexion Nouveau Sujet
Algorithme et fonctions racines carrés
Bonjour,
Énoncé :
Problème Le plan est muni d'un repère orthonormé. L'unité graphique est 1 cm
1) Etudier le sens de variation de la fonction définie sur par f(x)= 4-x²
4-x²
On nomme A l'aire de la partie du plan située entre l'axe des abscisses, l'axe des ordonnés et la courbe Cf représentative de f.
Partie A : détermination approchée de l'aire A
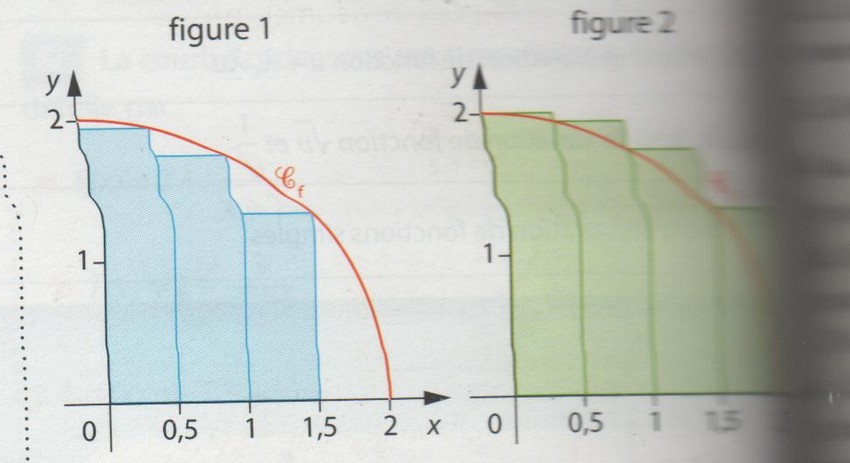
1) On trace des rectangles comme indiqué ci-dessous : Figure 1 figure 2 [ Voir Figure]
a) Justifier que la somme des aires des rectangles de la figure 1 est 1/2[f(0,5)+f(1)+f(1,5)]
b) Exprimer que la somme des aires des rectangles de la figure 2 et en déduire un encadrement de A
2) a) Faire les figures analogues pour des rectangles de largeur 0,25
b) En déduire un nouvel encadrement de A
3) a) Ecrire un algorithme qui permette d'obtenir un encadrement de A grâce à des rectangles de largeur 0,001 ?
b) Programmer cet algorithme
c) Quel encadrement de A obtient-on ?
Partie B/ Determination exacte de A
1) Justifier que ( Cf ) est une portion de cercle
2) En déduire la valeur exacte de A
Résolution:
1) F est strictement décroissante sur l'intervalle [0,2]
Partie A
1) a) Ici la longueur d'un rectangle esy egale à f(x) et sa largeur à 0,5.
On a donc A = 1/2xf(0,5)+1/2x(1)+1/2xf(1.5)
b A2= 1/2[f(0)+f(0.5)+f(1)+f(1.5)
A est donc compris entre 1/2[f(0,5)+f(1)+f(1.5)] et 1/2[f(0)+f(0.5)+f(1)+f(1.5)
2) A est compris entre 1/4[f(0.25)+f(0.5)+f(0.75)+f(1)+f(1.25)+f(1.5)+f(1.75) et 1/4[f(0)+f(0.25)+f(0.5)+f(0.75)+f(1)+f(1.25)+f(1.5)+f(1.75)
Puis pour l'algorithme c'est là où je bloque je ne suis pas doué pour les algorithmes, pourriez vous m'aider. Et je voudrais aussi savoir si le début est bon et aussi je n'arrive pas à faire la partie B.
Merci de votre compréhension.
Jai besoin de l aide les autres choses jai compris et jai reussi. Juste l'algorithme s'il vous plait j'ai demandé à des adultes mais c'est quelque chose de nouveau. Il y a que vous qui pouvait m'aider.
Bonjour,
Un peu méchant de demander l'algorithme sans avoir fait une petite généralisation "théorique" avant ...
je vais appeler h la largeur des rectangles
la première méthode donne donc en général :
(1/2)(f(h) + f(2h) + f(3h) + ..... ) jusqu'à plus soif c'est à dire tant que le x = n fois h est plus petit que 2
l'exemple numérique traité précédemment était avec h = 0.5
(1/2)(f(0.5) + f(1) + f(1.5)) et c'est fini car le pas suivant ammènerait à x = 2.
cela donne directement l'algorithme !!!
variables :
h (demandée tant qu'à faire plutot que bloquée rigidement à 0.001)
x valeur courante
S cumul
algorithme :
demander h
S=0
x=h
tant que x < 2
calculer f(x)
S + f(x)/2 --> S
x+h --> x
fin tant que
afficher S
on peut programmer cet algorithme sur une machine au choix en l'absence de consigne de l'énoncé (Algobox, calculette etc )
il faut bien entendu adapter la "syntaxe" à la machine utilisée
comme h est demandé et non pas fixé à 0.001 on peut tester l'algorithme avec h = 0.5 et vérifier qu'on obtient bien la valeur calculée à la main dans la question d'avant ...
(enfin qui aurait dû être calculée et pas laissée sous la forme paresseuse de la recopie de l'énoncé : on demande un encadrement pas une "formule bateau". encadrement c'est calculer effectivement la valeur numérique)
une fois cette première étape franchie il s'agit d'effectuer pareil pour la deuxième méthode (fig2)
en fait il suffit de changer juste quelques petits détails à l'algorithme précédent ...
l'étape suivante sera de mélanger les deux en un seul, qui calcule simultanément la borne inférieure S1 et la borne supérieure S2
et qui affiche l'encadrement S1 < S < S2
à toi de jouer, déja avec le premier algorithme, (le traduire et le tester) puis le transformer pour qu'il fasse le deuxième calcul, et tester ce deuxième algo
on verra après pour les deux en un.
OOPs 
la formule générale est pas du tout ça mais
h(f(h) + f(2h + f(3h) + ...)
(la valeur test h = 0.5 = 1/2 m'avait induit en erreur)
détail facile à corriger.
normallement plus on diminue h et plus la valeur résultat est proche de l'aire exacte qu'il est facile de calculer puisque c'est un quart de cercle de rayon 2,
soit 
 2²/4 =
2²/4 =  = 3.14159265358979...
= 3.14159265358979...
Ok merci pour l'algorithme mais lorsque vous me dites S+f(x)/2--->S. Cela se traduit en langage algorithmique S prend la valeur S+f(x)/2.
C'est bien ça ?
Je vous remercie encore pour l'algorithme. Pour les valeurs bateaux je les ai calculé c'est bon. 
variables : x,
demander h
S=0
tant que x < 2
calculer f(x)
S + f(x)/2 prend la valeur S
x+h prend la valeur x
fin tant que
afficher S
il faut juste changer le signe.
Je ne sais pas si cest S prend la valeur S+f(x)/2 ou cest S+f(x)/2 prend la valeur S. Je sais juste le dire en language Ti. S+f(x)/2 ->(stocké dans) S
pour l'algorithne de la figure 2 est ce qu'il est bon pour que je puisse les combiner
Mince excuser moi pour l'algorithme jai mi le signe du mauvais coté :
variables : x ,h,S
S=0
x=h
tant que x > 2
calculer f(x)
S + f(x)/2 prend la valeur S
x+h prend la valeur x
fin tant que afficher S
figure 2
Mince excuser moi pour l'algorithme jai mi le signe du mauvais coté :
vu les multiples hésitations, la version corrigée est :
variables : x ,h,S
S=0
x=h que vaut h ????
demander h (en Algobox c'est "LIRE h", en TI truc je ne sais pas)
S = 0 c'est comme "S prend la valeur" restons cohérent tout du long
donc :
variables : x ,h,S
debut algo :
lire h
S prend la valeur 0
x prend la valeur h
tant que x < 2 le sens était bon la première fois. "tant que" c'est du français ! "tant que ce n'est pas fini on continue"
calculer f(x) ici "f(x)" c'est sqrt(4 - x*x) mon algo était général pour une fonction f quelconque, mais "calculer" ne veut rien dire ici, il faudrait créer une nouvelle variable pour le résultat de ce calcul !
S + f(x)/2 prend la valeur S non. en terme de "prend la valeur" c'est :
S prend la valeur S+ ...
de plus j'avais déja signalé que le "divisé par 2" est faux.
c'est multiplié par h qu'il faut faire :
S prend la valeur S + h*f(x)/2
et pour éviter le calcul de f à part dans une variable de plus, on le met directement ici :
S prend la valeur S + h*sqrt(4 - x*x)
x+h prend la valeur x idem c'est :
x prend la valeur x + h
fin tant que
afficher S
fin algo
Oui donc le changement etait S prend la valeur S+h*f(x) alors que dans la figure 1 c'est S prend la valeur S+h*f(x)/2.
non.
c'est la même formule mais h = 1/2
la figure 1 est un exemple avec largeur des rectangles (h) = 0.5 et uniquement cette valeur là.
ici on veut mettre h = 0.001 c'est à dire 2000 rectangles de largeur 0.001
chacun aura comme aire 0.001*f(x) pour x = 0.001, 0.002, 0.003 .... 1.999
tu vois d'où il sort le "1/2" de la formule initiale ? les rectangles avaient pour aires
0.5*f(x) pour x = 0.5, 1.0, 1.5 l'écriture de ce 0.5 en 1/2 est source de piège, la preuve, j'étais tombé dedans à pieds joints.
et dans la question 2a ou on prend une largeur de 0.25
les rectangles ont pour aire 0.25*f(x) pour x = 0.25, 0.5, 0.75, ...1.75
dans tous les cas ce sera h*f(x) pour x = h, 2h, 3h, ... 2-3h, 2-2h, 2-h
l'algorithme écrit ici donne S1
il faut imaginer faire pareil avec S2, mais avant d'écrire quelque algorithme que ce soit qui calculerait S2, il serait bon d'écrire ça "mathématiquement" et en particulier de calculer algèbriquement la différence S2 - S1 (par les formules)
On sait que S2 est superieur a f(x).
S2 est une valeur numérique, y apas de x là dedans
non, écris :
S1 = h.f(h) + h.f(2h) + h.f(3h) + .... + h.f(nh) )
écris maintenant la formule équivallente pour S2 ...
quelle en est le 1er terme ? le dernier ?
aides toi des exemples avec h = 0.5 et surtout 0.25 (pas assez de termes avec h=0.5 pour raisonner sainement)
Ah ok ! Je croyez que vous attendez une soustraction quand vous m'avez difference  .
.
Alors la difference c'est que pour n'importe quelle valeur h la premiere valeur de S2 sera f(0) alors que la valeur de S1 sera f(h). Donc S2 aura toujour une valeur en plus de s1 qui sera f(0) mais les autres valeurs seront les memes valeurs que S1
c'est presque ça. (selon que tu as mis ou non h en facteur de tout)
tu vas donc avoir S2 = S1 + h.f(0) !
donc connaissant S1 il est facile de calculer après coup S2 et de rajouter juste une ligne ou deux à la fin de l'algorithme pour calculer S2 = S1 + h.f(0) et afficher S2
(bien sur ici f(0) tu en connais la valeur, hein ...)
Donc l'algorithme:
variables : x , S ,h ,n
S prend la valeur 0
x prend la valeur h
tant que x < 2
S prend la valeur S + h*(racine de 4-x*x)
x+h prend la valeur x
fin tant que
S+h*(racine de 4-x*x)*0 prend la valeur n
afficher S
Afficher n
Pas sur pour la fin..
encore un "expression prend la valeur variable" ???
de toute façon c'est "variable prend la valeur expression" !!!
bon S2 tu l'a appelé n, pourquoi pas.
mais le calcul c'est "n prend la valeur S + h*f(0)"
pas "n prend la valeur S + h*f(x)*0" qui fait S + 0 quoi qu'il arrive !!!
c'est quoi f(0) ??????
PS : méfies toi aussi de "racine de 4 - x*x" qui veut dire (racine de 4) - x*x
il faut écrire racine de (4 - x*x)
c'est bien ce que je craignais, d'où ma demande de précision ...
mais le calcul c'est "n prend la valeur S + h*f(0)"
f(0) c'est 2, cela donne
"n prend la valeur S + h*2"
y a plus de 'f' là dedans, tu a mis sa valeur : 2 !
(j'avais bien vu que ton h*f(x)*valeur était "bizarre" hein ... quelle que soit cette valeur, que ce soit 0 ou 2, ça n'a rien à faire là)
Ok cest bon je l'ai testé il fonctionne ! Bah cest bon on a fini je crois..
je te remercie pour ton aide mathafou 
bonsoire, j'ai le même Dm et j'arrive pas trouver la a et b du partie B
a.Justifier que Cf est une portion de cercle
b.En déduire la valeur exacte de A

Bonsoir, j'ai le même DM également je n'arrive pas le programme sur algobox il ne fonctionne pas alors que j'ai fait exactement comme ci-dessus et la partie je n'y arrive pas non plus.
Bonjour,
tu devrais te faire embaucher chez Microsoft avec un tel message d'erreur.
toi c'est pareil
parmi la foule de programmes faux, à moitié corrigés, pas complètement traduits en Algobox mais seulement "en langage naturel" qu'il y a dans ce topic on se demande lequel est celui "exactement comme ci-dessus"
et surtout j'adore le diagnostic extrêmement précis "ça marche pas"
il peut y avoir une foule de raisons pour laquelle ton programme ne marche pas
tu n'as pas pris le bon
tu as fait des fautes de frappe
tu n'as pas respecté la syntaxe précise d'Algobox (virgules au lieu de point décimal, symbole de multiplications etc.)
et la partie je n'y arrive pas non plus.
sans aucune précision sur ce qui te bloque et précisément ce que tu as fait tu ne risques pas d'avoir de l'aide pertinente.


