Inscription / Connexion Nouveau Sujet
algorithme et probabilité: lancer de dé
1) On lance 10 fois une pièce supposée équilibrée et on note à chaque lancer le côté PILE ou FACE obtenu.
Quelle est la probabilité d'obtenir :
a) le premier PILE lors du 2e lancer ?
b) le premier PILE lors des 4 premiers lancers ?
2) On lance dorénavant n fois la pièce ( n ≥ 2 )
a) Exprimer en fonction de n la probabilité Pn d'avoir au moins un PILE lors des n lancers .
b) Ecrire un algorithme qui détermine la première valeur de n tel que Pn ≈ 1 à 10-6 près .
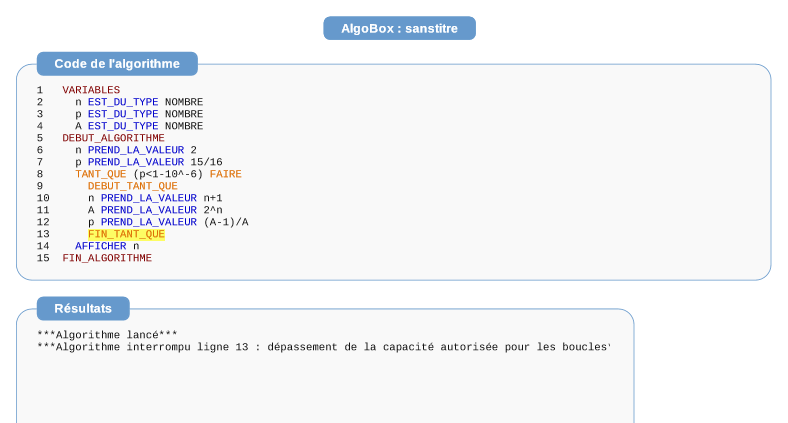
j'ai fais toutes les premières questions mais je bloque à l'algorithme. J'ai entré sur Algobox l'algorithme suivant:
n prend la valeur 2
p prend la valeur 15/16
tant que p < 1-10^-6 faire
debut tant que
n prend la valeur n+1
.. A prend la valeur 2^n
.. p prend la valeur (A-1)/A
fin tant que
afficher n
fin prog
Le probléme c'est que quand je teste l'algorithme, ca me donne "algorithme interrompue ligne fin tant que : dépassement de la capacité autorisé par les boucles"
Un peu d'aide svp?
Bonjour à toi aussi!
dans ce que tu as écrit p tend vers 1 et pas vers 0; donc forcément ta boucle ne peut pas se terminer.
je sais que ca n'a rien à voir mais quelqu'un ici s'y connaît en algorithme?
*** message déplacé ***
non je ne vois pas d'erreur grossière... il est possible que démarrer avec n=2 entraîne un décalage au final du résultat, mais sinon rien qui explique que cela tourne en boucle éternellement!
si on le faisait sans algorithme, on calculerait p(3), puis
p(4), puis p(5), etc... jusqu'à trouver une proba p> 1 - 10^6
je crois que n=20 convient parce que j'ai fait le calcul et 2^20 - 1 / 2^20 > 0,999999 !
Bonsoir,
Je n'ai pas ALGOBOX sur cet ordi donc je ne peux pas vérifier.
Mais de mémoire il existe une fonction POWER quand on veut élever à la puissance...
Donc je doute que 10^-6 soit valable.
Je te conseille de commencer par écrire :
pmin = 0.999999
Et d'afficher pmin au début du programme.
Et dans ta condition tu écris : Tant que (p < pmin) ...
Et d'une manière générale, quand on veut trouver ce genre d'erreur on affiche la valeur des variables...
L'erreur était donc bien dans la "traduction" avec ce 10^-6 qui ne veut pas dire ce que l'on souhaite; ce qui est étonnant cependant c'est que en faisant tourner algobox ne déclare pas une erreur sur la ligne correspondante....
Bonne continuation.
Bonjour,
on peut aussi remarquer que ;
ça donne un algorithme simplifié:
1 VARIABLES
2 n EST_DU_TYPE NOMBRE
3 DEBUT_ALGORITHME
4 n PREND_LA_VALEUR 1
5 TANT_QUE (pow(2,n)<pow(10,6)) FAIRE
6 DEBUT_TANT_QUE
7 n PREND_LA_VALEUR n+1
8 FIN_TANT_QUE
9 AFFICHER n
10 AFFICHERCALCUL pow(2,n)
11 FIN_ALGORITHME
Résultats
***Algorithme lancé***
20
1048576
***Algorithme terminé***
Bonjour,
on peut aussi remarquer que
ça donne un algorithme simplifié:
1 VARIABLES
2 n EST_DU_TYPE NOMBRE
3 DEBUT_ALGORITHME
4 n PREND_LA_VALEUR 1
5 TANT_QUE (pow(2,n)<pow(10,6)) FAIRE
6 DEBUT_TANT_QUE
7 n PREND_LA_VALEUR n+1
8 FIN_TANT_QUE
9 AFFICHER n
10 AFFICHERCALCUL pow(2,n)
11 FIN_ALGORITHME
Résultats
***Algorithme lancé***
20
1048576
***Algorithme terminé***
( n ≥ 2 )