Bonjour,

il y a plusieurs erreurs
une première de syntaxe (parenthèse absente dans une expression, erreur semblable d'ailleurs à l'erreur d'écriture ici : les parenthèses c'est pas pour décorer)

le reste est des erreurs de principe : même si ton programme "tournait" il donnerait du n'importe quoi comme résultat, si tant est qu'il s'arrête de boucler un jour...

- on cherche n
alors "LIRE n" ???? tu connais déja la valeur de n que tu cherches ???

- tu calcules en fait les Vk (j'appelle l'indice volontairement k et pas n)
pour k = de n en n (avec n la valeur que tu as saisie)
si tu saisis n = 5 par exemple, tu calcules V5 puis V10 puis V15 etc
(aucune des valeurs intermédiaires n'est utilisée à quoi que ce soit)
la boucle "pour" est totalement inutile : tout doit être fait dans la seule boucle tant_que

- ton test sur "tant que" est faux
on teste "tant que ce n'est PAS fini", tant que la condition qu'on cherche à avoir est fausse.
dans le tant que on écrit donc la négation de la condition que l'on cherche à obtenir : que valeur absolue de Vn - L soit inférieure à 10^-9.
la négation de cette condition est donc : tant que valeur absolue de Vn - L est supérieure ou égale à 10^-9.
valeur absolue à moins de démontrer que la suite est strictement monotone et de faire attention au sens dans lequel on calcule cette différence (pour obtenir quelque chose de toujours >0)

- de plus on ne veut pas que ce soit inférieur à 10 mais à 10^-9
(en algobox, les puissances s'écrivent avec la fonction pow())

Merci beaucoup pour votre réponse mathafou!

Alors j'ai modifié mon algorithme avec les instructions que vous m'avez donné. Mais il doit toujours être faux car lorsque je l'exécute il me dit: "interrompu ligne 13 : dépassement de la capacité autorisée pour les boucles***".


Je n'arrive pas a voir mon erreur et je ne comprends surtout rien aux algorithmes...

Bonjour,

En l'absence de mathafou, je vais reprendre sa première remarque :

Oui. Mais je ne comprends pas. Il faut donc que je rajoute une ligne avec Vn prend la valeur de (2*Vn-1+3)/(Vn-1+1)? Que faut il saisir alors?

NONONONONONON

Il suffit juste de prendre une variable V qui va prendre comme valeur

-2 au premier rang

puis

?????? au rang suivant ..... je mets des ???? parce que je n'ai toujours pas compris comment est définie la suite (V_n) .... manque cruel des parenthèses !!!!

Il n'y a rien à saisir puisque , ici , toutes les infos nécessaires à la résolution du problème sont connues de toi (pas forcément de nous)  !!! :
On connait la valeur du premier terme de la suite ...
On est sensé connaitre l'expression qui définit la suite
On cherche à partir de quel rang n la valeur de ..... est ....  10_-9


Il y aurait un truc à saisir (p) si on te demandait  partir de quel rang la valeur de ..... est .... 10_-p

pardon

Il n'y a rien à saisir puisque , ici , toutes les infos nécessaires à la résolution du problème sont connues de toi (pas forcément de nous)  !!! :
On connait la valeur du premier terme de la suite ...
On est sensé connaitre l'expression qui définit la suite
On cherche à partir de quel rang n la valeur de ..... est ....  10^-9


Il y aurait un truc à saisir (p) si on te demandait  partir de quel rang la valeur de ..... est .... 10^-p

Bonjour,

Pour une bonne utilisation des parenthèses voir ligne 14.

On peut remplacer la ligne 7 par lire n.

1   VARIABLES
2     n EST_DU_TYPE NOMBRE
3     v EST_DU_TYPE NOMBRE
4     p EST_DU_TYPE NOMBRE
5     old EST_DU_TYPE NOMBRE
6   DEBUT_ALGORITHME
7     n PREND_LA_VALEUR 5
8     p PREND_LA_VALEUR pow(10,-n)
9     old PREND_LA_VALEUR 100
10    v PREND_LA_VALEUR -2
11    TANT_QUE (abs(old-v)>p) FAIRE
12      DEBUT_TANT_QUE
13      old PREND_LA_VALEUR v
14      v PREND_LA_VALEUR (2*v+3)/(v+1)
15      AFFICHER v
16      FIN_TANT_QUE
17    AFFICHER "v="
18    AFFICHER v
19  FIN_ALGORITHME

Bonjour,

on ne demande pas la valeur de la limite à 10^-m près
mais à partir de quel rang n est-on plus près de la limite que 10^-m (et même l'énoncé précise ni 10^-5 ni 10^-m mais 10^-9)

j'ai appelé ça m pour éviter des confusions
confusion entretenue en appelant "n" la précision alors que n serait d'après l'énoncé le rang de V_n

certes les variables on peut les appeler comme on veut
rebaptiser le rang n en "q", la suite V_n en "x", utiliser "n" pour n'importe quoi d'autre etc

mais ça rendra l'algorithme absolument illisible, même s'il fonctionne

TANT_QUE (abs(old-v)>p) FAIRE
là tu cherches non pas quand la suite sera à 10^-n près de sa limite
mais quand deux termes successifs seront écartés de moins de 10^-n
ce qui n'a rien à voir,
en particulier on pourrait parfaitement avoir une suite monotone qui converge si lentement que l'écart entre deux termes successifs soit énormément inférieur à l'écart entre ces termes et la limite.
on aurait alors deux termes successifs écartés de moins de 10^-9 bien avant qu'ils ne soit aussi près que ça de la limite.

si la suite est alternativement < L et > L, on sait que la limite est entre deux termes successifs et donc que s'ils sont écartés de moins de 10^-9, alors la limite est encore plus près d'eux ("entre" = au pire au milieu)

mais pour utiliser cette propriété, il faut la démontrer d'abord !
et si elle est fausse (si la suite est monotone) alors on ne peut pas utiliser ce critère et on doit obligatoirement comparer à la valeur exacte de la limite (en fait valeur elle même approchée à une précision meilleure que 10^-9)

Que l'on écrive ou  , on obtient

une suite qui diverge vers !!!

En plus, si on remplace par ;       devient une limite possible , mais dès le rang 2 ou 4 on divise par 0!!! N'importe quoi!

il faut bien entendu être capable d'imaginer où les parenthèses qu'aurait absolument dû mettre schnecke on été "oubliées"
en effet schnecke SAIT le faire (il l'a fait, sauf oubli d'une seule parenthèse fermante, dans le programme Algobox !!)
ce qu'il n'a pas compris c'est qu'il faut obligatoirement quand on écrit tout en texte sur une seule ligne dans l'énoncé faire pareil que dans un programme ou sur une calculette :
ajouter obligatoirement des parenthèses !!
pour exprimer


comme V_n = 2Vn-1 + 3/Vn-1+1

ces parenthèses étant

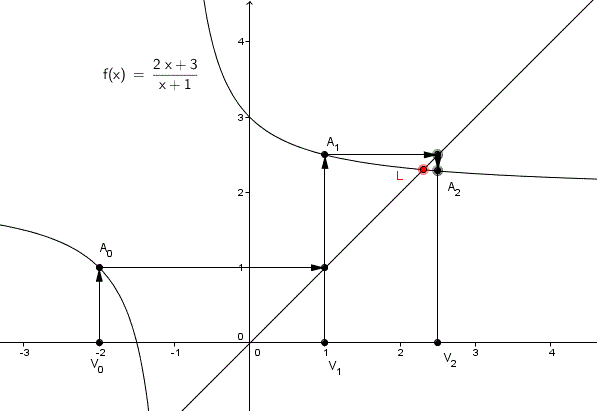
et alors la suite, en partant de V₀ = -2, converge bien vers une limite L qui est la solution >0 de L = (2L+3)/(L+1)

plus lisible (\dfrac et indices par X₂ oubliés)



comme V_n = 2V_n-1 + 3/V_n-1 +1