bonjour,

as tu fais un schéma pour mieux comprendre l'énoncé ?
En ligne 6 (le TANT QUE), on écrit la condition pour continuer à avancer.
NB : on avance tant qu'on n'a pas fait 5 pas et tant qu'on est sur la passerelle.

quelles conditions  doit on  écrire en ligne 6 :  
x représente le nombre de pas sur la passerelle (déplacement sur la longueur de la passerelle)
à ton avis, quelle est la valeur maxi pour x ?
y représente le déplacement sur la largeur de la passerelle. Puisque la passerelle fait 2 pas de large,quelles sont les valeurs mini et maxi pour y ?  

J'y avais pas pensé ! Je suis bête dis-donc ! xD Et oui, y avait un schémas mais j'ai pas pu le mettre en copie-colle ^^''
Merci pour le coup de main, je vais essayer ^^

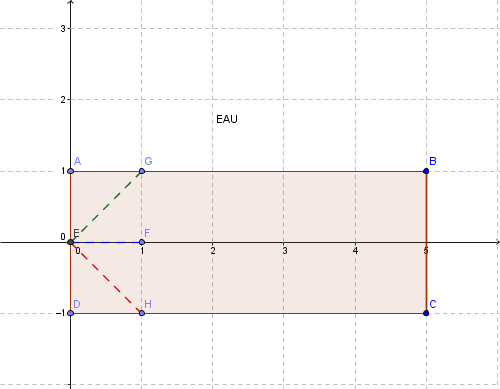
voici un schéma : le candidat au départ est en E(0;0)  
(NB : on a bien au début  
4. Affecter à x la valeur 0
5. Affecter à y la valeur 0 )

Il fait un premier pas (que devient y ? que devient x ? ),
si n = -1, il va en H  (et H(1 ; -1)  donc x a augmenté de 1 et y a pris la valeur y + n)
si n=1, il va en G  (et G(1 ; 1) )
si n= 0, il va en F  (et F(1; 0)

essaie  d'imaginer ce qui se passe au deuxième pas.  

je dois m'absenter : je reviens voir tout a l'heure si tu as pu continuer.
OK ?  

J'ai fait ceci :

1. Variables
2. x, y, n : entiers
3. Traitement
4. Affecter à x la valeur 0
5. Affecter à y la valeur 0
6. Tant que y =1 et y =-1 et x < ou = 5
7. Affecter à n un entier aléatoire
8. parmi -1 ; 0 et 1
9. Affecter à y la valeur y + n

Mais pour x je vois pas. :/

Ah peut-être que c'est ça :

10. Affecter à x la valeur 1
11. Fin tant que
12. Si x= 5

etc...

cela devrait être bon non ?

Au final, je pense que c'est mieux comme ça :

9. Affecter à x la valeur de x + n
10. Fin tant que
11. Si x=5
12. Alors, etc...

Et à partir de là, je commence à perdre l'air ^^'

ligne 6  :   on es sur la passerelle TANT QUE   y -1  et y 1    et x 5
Si tu écris y=-1  ET  y=1 , ça ne se produira jamais. y ne peut pas etre à la fois = -1 et = 1

ligne 9 : OK     y prend la valeur y+n

ligne 10 : regarde le schéma. Que fait la valeur de x à chaque pas ?
au départ, x=0.
je fais un pas, x=1    je fais encore un pas, x=2...    je fais encore un pas x=3..
toi tu écris x prend la valeur x+n  ==> quand n=0, tu n'avances pas, et quand n=-1, tu recules... ça ne peut pas être ça.

ligne 10 : x prend la valeur x+1

ligne 12 : OK      si x=5 alors

ce qui donne :

1. Variables
2. x, y, n : entiers
3. Traitement
4. Affecter à x la valeur 0
5. Affecter à y la valeur 0
6. Tant que y -1 et y 1 et x 5 faire  
7. Affecter à n un entier aléatoire
8. parmi -1 ; 0 et 1
9. Affecter à y la valeur y +n
10. Affecter à x la valeur x+1
11. Fin tant que
12. Si x = 5alors
13. Afficher « le candidat a traversé »
14. Sinon
15. Afficher « le candidat a perdu »
16. Fin si
17. Fin de l'algorithme

Bonjour,

En attendant le retour de Leile que je salue :
Dans cet algorithme x est la longueur ( 5 pas : si x=5 la passerelle est traversée) et y la largeur (2 pas : y peut être égal à -1 , 0 ou +1 sans tomber de la passerelle )
le candidat doit "avancer" d'un pas en avant, en 9  il faut x=x+1

la condition 12. si x=...parait insuffisante (il faut aussi vérifier y pour le pas de x=4 à x=5)

bonjour vham,
que penses tu de la question 2 ? pour moi, aucun de ces couples ne peut etre obtenu avec l'algorithme (ce sont des couples (x;y)...) ? Je suis surprise de l'énoncé..

Merci pour ta correction Leile ! Je suis contente de voir que je me suis pas trompée sur tout ! x) Et Vham, la condition en 12 est noté comme tel dans mon énoncé ^^' je ne peux pas rajouter la condition pour y.

Cette question 2 m'a un peu perturbée parce que l'algorithme est fait pour 10 déplacements donc je me suis posée des questions, mais ça n'a pas l'air cohérent, donc j'ai pas compris ^^'

(10;0) marche je pense, car l'algo est sur 10 déplacements.

Les autres ne marchent pas car le TANT QUE du y n'est pas respecté (je ne sais pas comment le décrire ^^'')

"l'algo est écrit pour 10 déplacements "   je n'avais pas fait attention à ça
dans ce cas, x maximum = 10  et pas 5 !

6. Tant que y -1 et y 1 et x 10 faire  
et
12. Si x = 10  alors

en effet, si x varie de 0 à 10  et y varie de -1  à  1 , alors on est sur la passerelle.
(−1 ; 1)  ==> impossible x ne peut pas etre négatif.
(10 ; 0) ==> possible (gagné)
(2 ; 4) ==>  impossible (on est tombé dans l'eau bien avant que y=4)
(10 ; 2) ==> possible : on tombe dans l'eau au 10ème pas.

tu as une idée pour la question 3 ?

Oui, je me disais bien pour l'algo' Leile. Mais j'ai rien compris à ce que tu as expliqué (enfin juste des petits trucs). Je n'ai jamais entendu parler du "marqueur Boolean" et je vais essayer avec le programme Python, mais je ne sais pas si c'est l'option que je vais prendre. Puisqu'il faut former l'algorithme sur notre calculatrice.

Et donc, pour la question 3, j'ai bien compris qu'il fallait faire recommencer l'algorithme un certains nombres de fois et donner la fréquence de traversée réussie, mais je ne sais pas (ou plus) comment faire ^^'

Bonjour,

il ne faut pas avoir x=6 donc on prend la condition x<=4.

1   VARIABLES
2     x EST_DU_TYPE NOMBRE
3     y EST_DU_TYPE NOMBRE
4     n EST_DU_TYPE NOMBRE
5   DEBUT_ALGORITHME
6     x PREND_LA_VALEUR 0
7     y PREND_LA_VALEUR 0
8     TANT_QUE (y<=1 et y>=-1 et x<=4) FAIRE
9       DEBUT_TANT_QUE
10      n PREND_LA_VALEUR ALGOBOX_ALEA_ENT(0,2)-1
11      y PREND_LA_VALEUR y+n
12      x PREND_LA_VALEUR x+1
13      FIN_TANT_QUE
14    SI (x==5 et abs(y)<=1) ALORS
15      DEBUT_SI
16      AFFICHER "traversé"
17      FIN_SI
18      SINON
19        DEBUT_SINON
20        AFFICHER "non traversé"
21        FIN_SINON
22    AFFICHER x
23    AFFICHER y
24    AFFICHER n
25  FIN_ALGORITHME

Résultats
***Algorithme lancé***
traversé
5
0
-1
***Algorithme terminé***

merci vham de ta réponse.
Je crois que ce sont les couples (x;y) avec x allant jusque 10.

tu as raison pour la ligne 6 la borne sur x doit etre x 9 (pour faire 10 pas  numérotés de 0 à 9), ce qui permet de tester x=10 en ligne 12

je suis d'accord avec toi sur le marqueur booleen, mais il s'agit de compléter l'algo existant, on n'a pas la liberté de changer le test.
De meme, perso, je n'aurais pas mis un test d'égalité en ligne 12..

La proba de rester sur la passerelle est trop faible (surtout avec 10 pas) ==> je ne m'y risquerai pas, moi.

Yuki812,
j'ai tapé l'algo en algobox,
en ajoutant une boucle POUR   : elle te permet d'effectuer la traversée N fois.
essaie de modifier ton algorithme en fonction de ça, et de calculer la fréquence de réussite.
je te donne l'algo ensuite. OK ?

Ok, merci, je vais essayer ^^

1   VARIABLES
2     x EST_DU_TYPE NOMBRE
3     y EST_DU_TYPE NOMBRE
4     n EST_DU_TYPE NOMBRE
5     M EST_DU_TYPE NOMBRE   ==>   c'est le nombre d'essais
6     F EST_DU_TYPE NOMBRE   ===> fréquence de réussite
7     I EST_DU_TYPE NOMBRE
8   DEBUT_ALGORITHME
9     x PREND_LA_VALEUR 0
10    y PREND_LA_VALEUR 0
11    F PREND_LA_VALEUR 0
12    LIRE M
13    POUR I ALLANT_DE 1 A M
14      DEBUT_POUR
15      x PREND_LA_VALEUR 0
16      y PREND_LA_VALEUR 0
17      TANT_QUE (y>=-1 ET y<=1 ET x<=9) FAIRE
18        DEBUT_TANT_QUE
19        n PREND_LA_VALEUR ALGOBOX_ALEA_ENT(0,2)
20        n PREND_LA_VALEUR n-1
21        y PREND_LA_VALEUR y+n
22        x PREND_LA_VALEUR x+1
23        FIN_TANT_QUE
24      SI (x==10) ALORS
25        DEBUT_SI
26        ///*** Gagné ****/
27        F PREND_LA_VALEUR F+1
28        FIN_SI
29        SINON
30          DEBUT_SINON
31          FIN_SINON
32      FIN_POUR
33    AFFICHER F
34    F PREND_LA_VALEUR F/M
35    AFFICHER F
36  FIN_ALGORITHME


***Algorithme lancé***
Entrer M : 10000

F = 0.1723
***Algorithme terminé***


tu vois ?

ha oui, d'accord, je comprends mieux ! Merci beaucoup !

Je ne comprends pas pourquoi on passe à 10 déplacements!!!

sinon:

1   VARIABLES
2     x EST_DU_TYPE NOMBRE
3     y EST_DU_TYPE NOMBRE
4     n EST_DU_TYPE NOMBRE
5     M EST_DU_TYPE NOMBRE
6     k EST_DU_TYPE NOMBRE
7     t EST_DU_TYPE NOMBRE
8   DEBUT_ALGORITHME
9     t PREND_LA_VALEUR 0
10    LIRE M
11    POUR k ALLANT_DE 1 A M
12      DEBUT_POUR
13      x PREND_LA_VALEUR 0
14      y PREND_LA_VALEUR 0
15      TANT_QUE (y<=1 et y>=-1 et x<=4) FAIRE
16        DEBUT_TANT_QUE
17        n PREND_LA_VALEUR ALGOBOX_ALEA_ENT(0,2)-1
18        x PREND_LA_VALEUR x+1
19        y PREND_LA_VALEUR y+n
20        SI (x==5 et abs(y)<=1) ALORS
21          DEBUT_SI
22          t PREND_LA_VALEUR t+1
23          FIN_SI
24        FIN_TANT_QUE
25      FIN_POUR
26    AFFICHER t
27    AFFICHERCALCUL t/M
28  FIN_ALGORITHME

Résultats
***Algorithme lancé***
Entrer M : 1000
403
0.403
***Algorithme terminé***

bonjour mathamore,
on passe à 10 déplacements parce que c'est ce qui est demandé dans l'énoncé :

"1) Compléter l'algorithme suivant pour qu'il simule la position du candidat au bout de 10 déplacements.

Bonjour,

Pour information dans le cas du problème présent :
Un calcul "simple" est bien meilleur qu'une suite de simulations donnant des valeurs "dispersées"

# Python version 3.
for xmax in range(5,11): # Longueurs x de 5 à 10
    p=[0,1,0] # probabilités initiales pour les 3 positions y possibles
    for x in range(xmax): # effectuer les x pas
        pancien,p=p[:],[0,0,0] # en préparant les nouvelles probabilités
        for y in range(len(p)): # à partir de chaque position y
            for i in range(-1,2): # aller à gauche, tout droit ou à droite
                if y+i>=0 and y+i<=2: # sans tomber
                    p[y+i]+=pancien[y]/3 # voilà la probabilité associée à ce pas
    print("si x=",x+1," la probabilité de traverser sans chuter =",sum(p)) 
  

Une autre illustration de ce que dit  vham...
Sur tableur, le calcul direct se fait en 3 minutes, en propageant les probabilités d'une case à une autre...



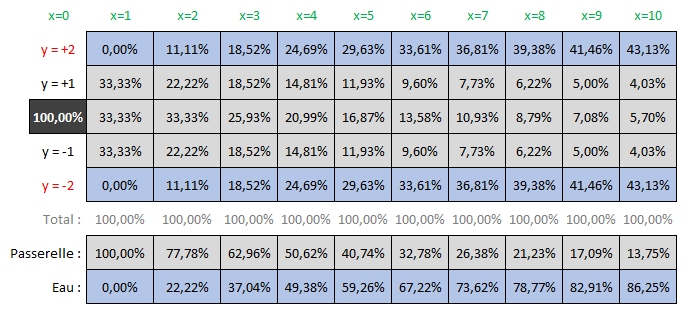
On part de la case x=0 y=0 avec certitude (P=100%), puis on progresse vers la droite (x=x+1) avec des probabilité  1/3  1/3  1/3 ...
La probabilité d'être encore sur la passerelle au dixième pas est de 13.75%...
... à comparer avec les résultats de simulation (qui seront très fluctuants...).

Bonsoir,

Comme je suis en accord avec LeDino !!
Aoprendre à se servir d'un tableur,
Apprendre à utiliser un VRAI logiciel, avec des commentaires significatifs qui suivent la pensée, c'est quand même mieux que faire jouer aux devinettes sur un algorithme mal présenté en AlgoBox ...

bonjour LeDino et vham,
oui, c'est sans doute mieux de faire autrement, mais ici, pour aider Yuki812 en respectant l'énoncé, qui dit "compléter l'algorithme suivant", il faut bien utiliser algobox...

Bonsoir,

Je ne conteste en aucun cas l'exercice donné qui est très intéressant.
Je conteste encore moins l'aide apportée qui est de grande qualité .
J'ai juste donné un coup de main en fournissant les vraies valeurs, qui aideront à valider l'algorithme.
Et montré qu'on peut arriver au résultat cherché par une autre méthode.
Mais cela ne dispense absolument pas de faire l'exercice comme il est demandé.

oui, oui, LeDino, je l'avais bien compris, pas de problème..

J'ai posté surtout pour rassurer Yuki812 après "utiliser un VRAI logiciel, avec des commentaires significatifs qui suivent la pensée, c'est quand même mieux que faire jouer aux devinettes sur un algorithme mal présenté en AlgoBox ..."

Bonne soirée.  

Bonsoir,

Mes commentaires de 17h02 sont un peu durs, mais, tout en étant navré d'insister sur ce que j'évoquais, voici le résultat de la transcription en Python de l'algorithme fourni par Leile à 12h58,
j'ai fait varier xMax de 5 à 11 et
quand Leile a mis x<=9 ligne 17, j'ai mis x<=xMax-1
quand Leile a mis x==10 ligne 24, j'ai mis if x=xMax
F/M = 0.5101   xMax = 5
F/M = 0.407   xMax = 6
F/M = 0.3271   xMax = 7
F/M = 0.2636   xMax = 8
F/M = 0.2138   xMax = 9
F/M = 0.1639   xMax = 10
F/M = 0.1374   xMax = 11
Les résultats fournis par mon programme Python de 17h02 sont conformes avec ceux produits par LeDino à 18h48
si x= 5  la probabilité de traverser sans chuter = 0.40740740740740744
si x= 6  la probabilité de traverser sans chuter = 0.3278463648834019
si x= 7  la probabilité de traverser sans chuter = 0.26383173296753537
si x= 8  la probabilité de traverser sans chuter = 0.21231519585429046
si x= 9  la probabilité de traverser sans chuter = 0.17085810089925313
si x= 10  la probabilité de traverser sans chuter = 0.13749597791664547

Que Leile veuille me pardonner si je montre que son algorithme donne pour x le résultat valable (approché en tant que simulation) pour x-1,
mathamore donne à 13h37 un résultat convenable avec son test ligne 20.

vham, c'est vrai, l'algo que j'avais proposé présente une erreur de borne ; il manque le dixième pas, apparemment.
Merci d'avoir corrigé.
Quant à l'outil, je ne connais pas python : est ce que les élèves l'apprennent ?  
Bonne nuit.

Bonjour,

Merci Leile d'avoir pris mes propos du bon côté.
Il y a 3 outils que les élèves devraient commencer à pratiquer dès la seconde, gratuits et de qulité :
Geogebra, Python et Xcas.